如何分享秘密？

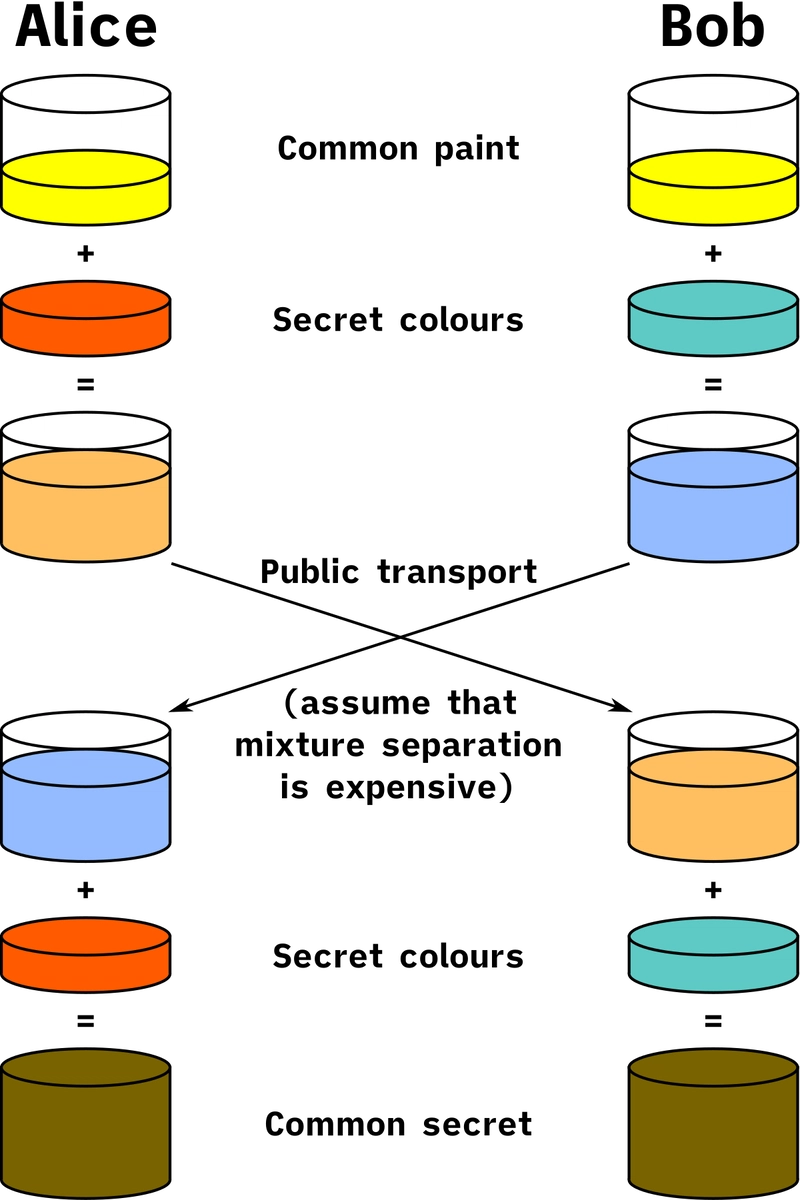
想象一下，你和一群完全陌生的人待在一个房间里，你可以大声地和其中一个人分享秘密信息，而其他人都在听。乍一听似乎不太可能，对吧？你怎么能大声说出只有那个人能听懂的话呢？好吧，你或许会用杜米语说话，希望只有那个人能听懂。但如果那个人听不懂杜米语呢？或者更糟糕的是，其他人听懂了，你的秘密突然泄露了怎么办？如果你能公开创造一种只有你和那个人才能理解的通用语言呢？这就是迪菲-赫尔曼密钥交换方法的用武之地。

迪菲-赫尔曼密钥交换

“Diffie-Hellman密钥交换方法允许互不相识的双方通过不安全的信道共同建立一个共享密钥。然后，该密钥可用于使用对称密钥密码加密后续通信。” - 维基百科

现在我们已经完成了正式定义，让我们来看看这究竟意味着什么。

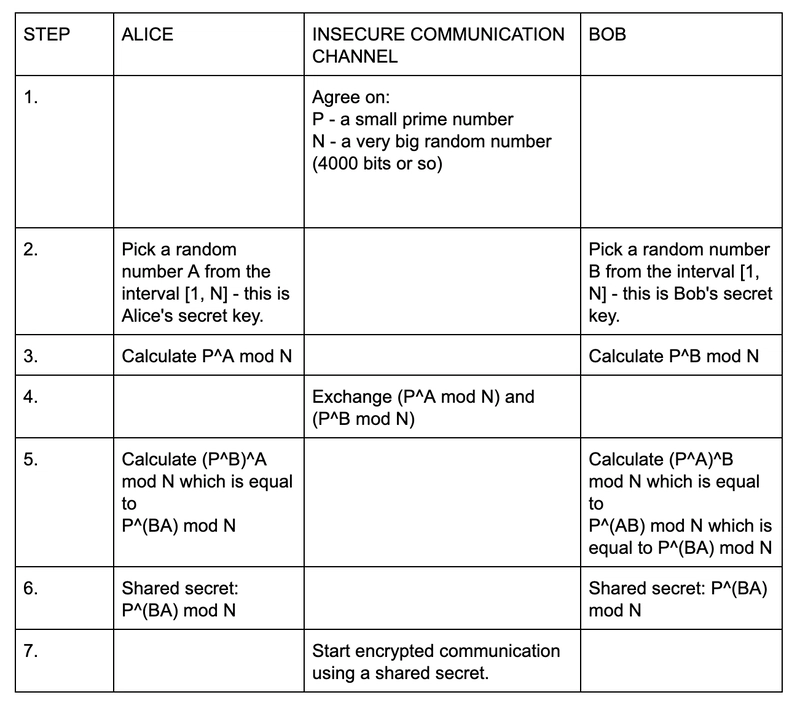
假设我们熟知的安全专家朋友 Alice 和 Bob 想要进行 Diffie-Hellman 密钥交换。第一步，他们就一些公开信息达成一致，我们称之为公共密钥，该密钥稍后将用于创建一个共享私钥——用于加密他们之间的所有通信。达成公共密钥一致后，他们各自创建一个私钥并保存。第三步，Alice 和 Bob 各自将公共密钥与自己的私钥组合，并公开交换该组合。这里最重要的假设是，几乎不可能将组合后的密钥还原为初始部分——公共密钥和私钥。否则，这种方法就失去了意义。你可能会问，这怎么可能呢？我们稍后会解释。
在交换组合之后（Alice 得到 Bob 的私钥和公共密钥的组合，反之亦然），他们再次各自将私钥与从对方那里得到的组合组合。完成此过程后，他们最终会得到同一个密钥，只有 Alice 和 Bob 知道这个密钥，然后使用该密钥对他们之间的通信进行加密。

迪菲-赫尔曼测试背后的数学原理

在本文的第一部分，我们以较为抽象的方式探讨了迪菲-赫尔曼比对法的工作原理。在这一部分，我们将深入了解迪菲-赫尔曼比对法的数学原理，以及这种方法是如何实现的。

在开始之前，我希望你们都熟悉模运算，但我们还是快速看一下。

a mod b（a 除以 b 的余数）是指 a 除以 b 的余数。
例如，11 mod 3 = 2，因为 11/3 等于 3 余 2。

你可以把模运算想象成绕着一个时钟转圈，时钟上的数字从 0 到 (b - 1)。根据上面的例子，时钟上的数字是 0、1、2，你要绕着时钟转 3 圈，最后停在数字 2 上。

现在我们准备看看在执行 Diffie-Hellman 测试时内部发生了什么。

还记得之前关于几乎不可能拆解私钥和公钥组合的假设吗？我们来看看第四步，也就是所有“魔法”发生的地方。
假设你是一个想要破解加密的攻击者。你只需要从 (P^A mod N) 或 (P^B mod N) 中找出数字 A 或 B（Alice 或 Bob 的秘密）。因为，如果你找到了 A，那么你就可以轻松计算 (P^B)^A mod N，从而得到共享秘密并破解加密。

乍听之下似乎很简单，但实际上即使对超级计算机来说也是个难题。这个问题被称为离散对数问题，无法在多项式时间内解决。你可以把这个问题的解决方法想象成一个穷举算法，它遍历 [1, N] 之间的所有数字，找到满足公式 (P^A mod N) 的数字，其中只有一个数字对应于实数 A。

在加密通信中，如何交换对称密钥始终是一个难题，因为非对称加密（一个密钥用于加密，另一个密钥用于解密）耗时较长，不适合快速通信。Diffie-Hellman 密钥交换是解决此问题的一种方法。另一种方法是使用非对称加密来加密和交换对称密钥，然后用该对称密钥对通信进行加密（用公钥加密对称密钥，使其只能用私钥解密）。例如，每次您通过 HTTPS 协议访问网站时，都会在所谓的 HTTPS 握手过程中进行这种密钥交换。

就这些啦！感谢阅读，如果有什么问题，欢迎在评论区留言。谢谢！:)