学习算法 - 二分查找

线性搜索

二分查找

大家好，如果你已经熟悉一些数据结构，现在是时候学习一些算法了。首先要介绍的是一个非常基础但非常重要的主题：二分查找。

我不用懂算法也能编程，为什么要费劲去学算法呢？

当然，从技术上讲，你可以不用算法也能开发软件，而且算法也不是必需的（我想应该是这样）。但是，当你解决软件问题时，你是否曾问过自己“我还能做得更好吗？”。这就是算法发挥作用的地方，最终，这种思考会让你成为一名更优秀的程序员。

让我解释一下为什么这很重要。

像 Facebook 这样的服务拥有超过 27 亿用户，这意味着 Facebook 的工程师们需要处理海量用户的数据。他们有两个程序 A和程序 B来处理这些数据。程序 A 处理每个用户的数据需要 1 秒，而程序 B 则需要 2 秒。这两个程序的速度差异是多少呢？其实不用计算，程序B 的耗时是程序 A 的两倍。

算法的核心在于如何高效地解决问题，而要做到这一点，你需要像计算机一样思考。
最常用的算法应用于搜索和排序，今天我将重点讨论搜索算法。

线性搜索

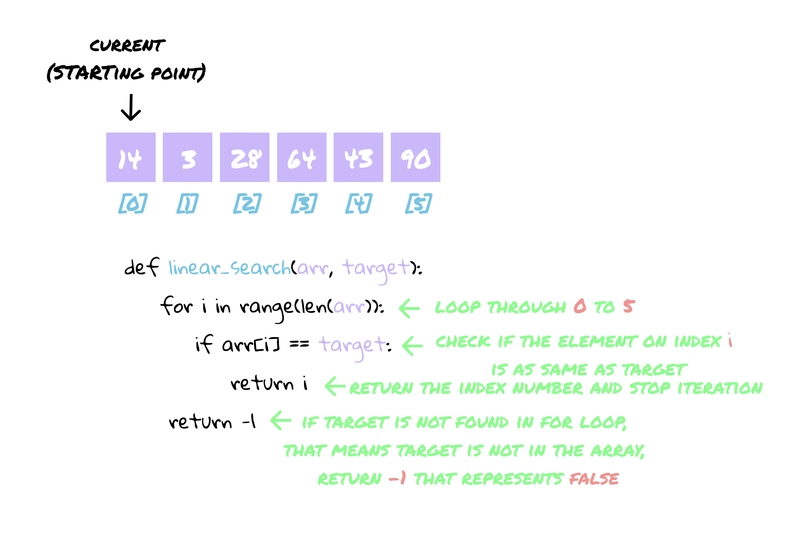
我们不能在不了解线性搜索的情况下直接学习二分查找。你应该熟悉这种算法，它使用从数组 0 到数组末尾的 for 循环来查找数组中的元素。它需要 n 次循环，因为每次循环都会检查目标元素是否在索引 0 到 5 之间。线性搜索的时间复杂度为O(n)。

它看起来还不错，但我们能做得更好吗？是的，我们可以通过使用二分查找
来改进它。

二分查找

它的工作原理与线性搜索类似，但区别在于，它会将数组减半，从而减少搜索范围，这意味着可以节省搜索时间，直到找到目标为止。

让我们看看这个算法在现实生活中是如何运作的。

你有一本字典要查一个词，你想查的是“glorious”。首先，你从中间翻开字典，现在你正好翻到了“glorious”这一M部分。其次，因为这一G部分在书的开头，所以不需要再往后翻M。第三，你又随意地从开头和M“glorious”之间翻开，现在你又翻到了F“glorious”这一部分，这意味着你需要在“ glorious”F和M“glorious”之间来回翻页，直到找到“glorious”这一G部分为止。你明白我的意思了吧。

基本上，它会不断缩小搜索范围，直到找到目标为止。

现在我们来深入探讨一下。我们要从43这个数组中找到一个数字[14, 3, 28, 64, 43, 90]。等等，我们不能直接使用二分查找，因为它是乱序的，根本无法确定查找范围！没错……只有当数组排序后才能进行二分查找。我们先来把它排序。

步骤 1. 所以，在这种情况下。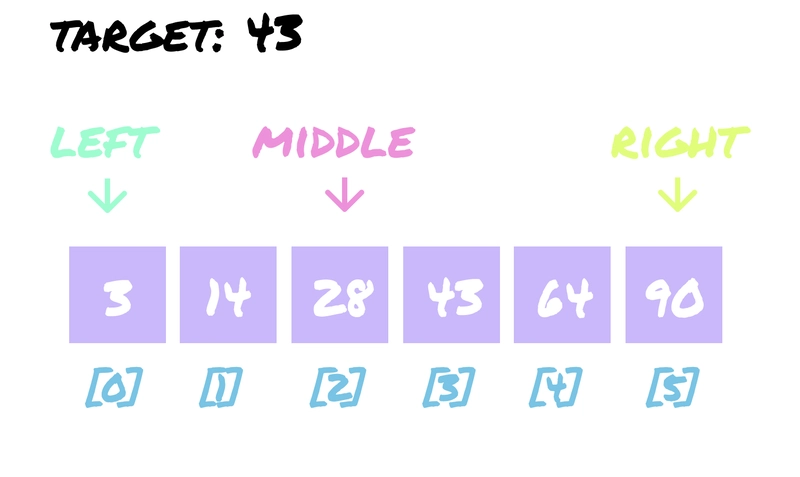

left = 0right = arr.lengthmid = (left + right) / 2

我们来检查一下当前中点是否是目标点。是28 == 43吗？不是！好的，那我们现在怎么办？因为28小于43，所以我们将left指针向右移动到中点。

步骤 2. 由于我们移动了左指针，指针现在应该再次位于左右中间，也就是。让我们再次检查是否找到了 43。是吗？不是！那么大于还是小于？大于。那么我们需要将右指针移动到中点左侧。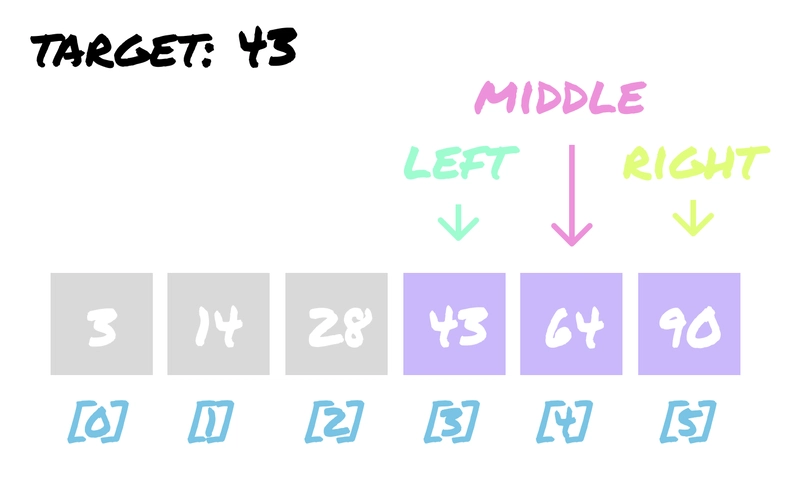

mid(3 + 5) / 2 = 4 ((left+right) / 2)64(middle) == 43(target)64436443

步骤 3. 现在，中点位于索引 [3]。所以中点是 3。但是如果 left + right 是一个不能被 3 整除的奇数呢？例如，如果 left + right 是3，那么用 3除以 3 得到 3 ，这不是一个可以用作索引的整数。如果您有 Python 编程经验，您需要使用整数除法器，例如 3，它会去掉小数点，然后返回 3。这样对吗？是的，对！让我们返回中点指针 3。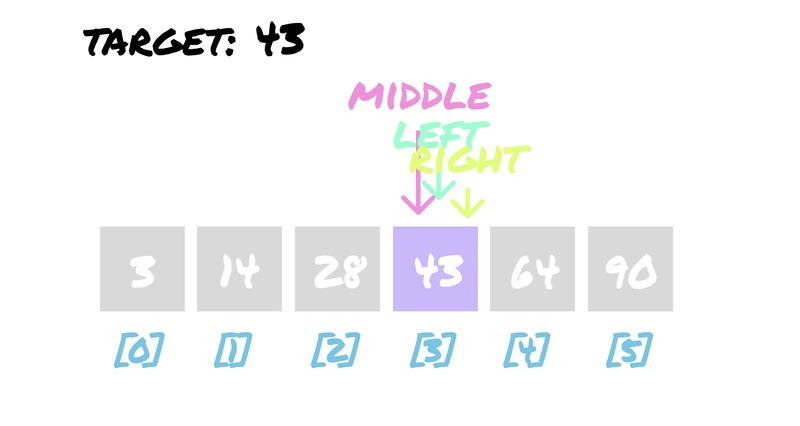

left + right = 66 / 2 = 3723.5left + right // 243(middle) == 43(target)

你用了多少步才找到 43？

我们走了 3 步，如果 n 是数组的长度，那么我们大约走了n/2步，这比线性搜索快得多，而且相对于N的大小，这步数还会更小。如果N非常大，最终我们将节省大量时间。因此，我们完成了 n 的一半工作量，可以表示为 1/2 * 1/2 * 1/2 * 1/2 * 1/2 = log5（假设对数以 2 为底）。因此，时间复杂度为O(log2N)。

执行

二分查找有两种实现方式：迭代法和递归法。为了简单起见，我将给出一个迭代法的实现示例。以下是类似 Python 的伪代码：

def binary_search(arr, target):
  left = 0
  right = arr.length - 1
  while left <= right:
    mid = (left + right) // 2
    # When found target
    if arr[mid] == target:
      return mid
    # When target is less than midpoint value
    elif target < arr[mid]:
      right = mid - 1  # move right pointer to left of mid
    # When target is greater than midpoint value
    else:
      left = mid + 1  # move left pointer to right of mid
  return -1

希望这篇文章对你的计算思维有所帮助，以后我会继续讲解算法！感谢阅读！