Rust 数据科学教程 1
[图片来自Unsplash的jim gade, 已修改] 数据科学:计算机科学的一个分支,研究如何使用、存储和分析数据,以便从中获取信息。
在本系列短片中,我们将探讨如何使用一些老旧的工具来完成任何数据科学家都必不可少的任务。
最终目标是展示 Rust 在该领域的应用,以及如何应用。我们的最终目标也是激发人们对该应用领域的兴趣:作者确信 Rust 在数据科学(以及机器学习和最终的人工智能)领域将非常有用。
您可以在以下代码库中找到本文的代码:github.com/davidedelpapa/rdatascience-tut1
本教程的背景介绍
本教程中我们将介绍的箱子种类不多,但我们会边讲解边介绍。
让我们以最传统、最粗糙的方式开始我们的项目吧。
cargo new rdatascience-tut1 && cd rdatascience-tut1
cargo add ndarray ndarray-rand ndarray-stats noisy_float poloto
code .
我目前使用cargo addcargo -edit(快速安装:)cargo install cargo-edit来处理依赖项,并使用Visual Studio Code作为开发 IDE。
您可以手动处理Cargo.toml依赖项,或者使用其他 IDE。
ndarray:它是什么,为什么要使用它?
ndarray是一个 Rust crate,用于处理数组。
它涵盖了数组处理框架(例如numpyPython 中的数组)的所有经典用法。一些主 crate 未涵盖的用例,则通过一些衍生 crate 来实现,例如用于线性代数的ndarray-linalg 、用于生成随机数的 ndarray-rand以及用于统计的ndarray-stats。
此外,它还具有一些不错的附加功能,例如通过其中一个可用的后端(使用blas-src)ndarray支持rayon进行并行化或流行的BLAS底层规范。
为什么要使用 ndarray?
Rust 中已经有了数组(或列表)和向量,而且该语言本身允许通过强大的迭代器进行多种不同类型的操作。
此外,Rust 语言本身(通过增强std)提供的功能比其他更流行的语言快很多倍;尽管如此,它仍然ndarray是专门处理 n 维数组的,其最终目的是数学上的应用。
因此,ndarrayRust 进一步增强了语言本身已有的强大功能;Rust 的强大功能是作者确信 Rust 将在未来几年成为数据科学语言的原因之一。
ndarray 快速入门
在src/main.rs文件的顶部,我们将像往常一样导入:
use ndarray::prelude::*;
序曲部分我们几乎已经具备了所有需要的条件。
我们可以开始往里面放东西了fn main()
创建数组
让我们开始学习如何创建数组:
let arr1 = array![1., 2., 3., 4., 5., 6.];
println!("1D array: {}", arr1);
ndarray提供了一个array!宏,用于检测所需的数据类型ArrayBase。在本例中,这是一个一维数组。请注意,底层ArrayBase已经实现了一个std::fmt::Display函数。
将其与标准的 Rust 数组(为了避免与 's 数组混淆,我们称它们为列表ndarray)和 Vec 进行比较:
// 1D array VS 1D array VS 1D Vec
let arr1 = array![1., 2., 3., 4., 5., 6.];
println!("1D array: \t{}", arr1);
let ls1 = [1., 2., 3., 4., 5., 6.];
println!("1D list: \t{:?}", ls1);
let vec1 = vec![1., 2., 3., 4., 5., 6.];
println!("1D vector: \t{:?}", vec1);
结果如下:
1D array: [1, 2, 3, 4, 5, 6]
1D list: [1.0, 2.0, 3.0, 4.0, 5.0, 6.0]
1D vector: [1.0, 2.0, 3.0, 4.0, 5.0, 6.0]
还要注意,它array!把浮点数写成了整数,因为它们都是整数.0。
数组求和
让我们尝试逐个元素地对两个数组求和:
let arr2 = array![1., 2.2, 3.3, 4., 5., 6.];
let arr3 = arr1 + arr2;
println!("1D array: \t{}", arr3);
让我们看看它与标准数组(列表)和向量相比如何:
let arr2 = array![1., 2.2, 3.3, 4., 5., 6.];
let arr3 = arr1 + arr2;
println!("1D array: \t{}", arr3);
let ls2 = [1., 2.2, 3.3, 4., 5., 6.];
let mut ls3 = ls1.clone();
for i in 1..ls2.len(){
ls3[i] = ls1[i] + ls2[i];
}
println!("1D list: \t{:?}", ls3);
let vec2 = vec![1., 2.2, 3.3, 4., 5., 6.];
let vec3: Vec<f64> = vec1.iter().zip(vec2.iter()).map(|(&e1, &e2)| e1 + e2).collect();
println!("1D vec: \t{:?}", vec3);
结果是:
1D array: [2, 4.2, 6.3, 8, 10, 12]
1D list: [1.0, 4.2, 6.3, 8.0, 10.0, 12.0]
1D vec: [2.0, 4.2, 6.3, 8.0, 10.0, 12.0]
正如你所见,使用 Rust 标准工具很快就会变得复杂。要逐个元素求和,我们需要一个 `______`for或(仅适用于 Vec)我们需要使用迭代器,迭代器功能强大,但在日常数据科学场景中使用起来却非常复杂。
二维数组及更多
让我们快速放弃使用 Rust 标准构造的示例,因为正如我们所展示的,它们更加复杂,让我们专注于ndarray。
ndarray提供创建、实例化(和使用)二维数组的各种方法。
看看这个例子:
let arr4 = array![[1., 2., 3.], [ 4., 5., 6.]];
let arr5 = Array::from_elem((2, 1), 1.);
let arr6 = arr4 + arr5;
println!("2D array:\n{}", arr6);
及其输出:
2D array:
[[2, 3, 4],
[5, 6, 7]]
使用宏时array!,我们需要指定所有元素;而使用时,Array::from_elem我们需要提供一个元素Shape(在本例中为 `<a>`)(2,1)和一个元素来填充数组(在本例中1.0为 `<a>`):它将使用选定的元素填充整个形状。
let arr7 = Array::<f64, _>::zeros(arr6.raw_dim());
let arr8 = arr6 * arr7;
println!("\n{}", arr8);
其输出结果为:
[[0, 0, 0],
[0, 0, 0]]
Array::zeros(Shape)Shape创建一个全部填充零的数组。
请注意,有时编译器无法推断要输入的零的类型(你差点忘了 Rust 有一个很好的类型系统,不是吗?),所以我们用注解来帮助它Array::<f64, _>,该注解给出类型,让编译器推断形状(_)。
正如你所想,该函数.raw_dim()给出了矩阵的形状。
现在我们来创建一个单位矩阵(一个二维数组,除对角线元素外,其余元素均为 0)。
let identity: &Array2<f64> = &Array::eye(3);
println!("\n{}", identity);
其输出结果为:
[[1, 0, 0],
[0, 1, 0],
[0, 0, 1]]
我们通过提供形状和类型信息帮助编译器,但这次使用的是特殊形式的 `int` ArrayBase,即Array2表示二维数组的 `int`。请注意,我们创建了一个引用,这样我们就可以重用该变量而不会引起借用检查器的注意(是的,它一直都在工作,你也忘了这一点吗?)。
现在我们来探讨一下单位矩阵的用途:
let arr9 = array![[1., 2., 3.], [ 4., 5., 6.], [7., 8., 9.]];
let arr10 = &arr9 * identity;
println!("\n{}", arr10);
输出:
[[1, 0, 0],
[0, 5, 0],
[0, 0, 9]]
我记得数学课上学过,单位矩阵乘以其他矩阵应该得到相同的矩阵……
当然,我们不是在进行点乘!普通的乘法运算是行不通的。
事实上,在使用矩阵时,既有逐元素乘法(通过 `a` 实现)arr9 * identity,也有矩阵乘法(通过 `b` 实现)。
let arr11 = arr9.dot(identity);
println!("\n{}", arr11);
最终输出结果为:
[[1, 2, 3],
[4, 5, 6],
[7, 8, 9]]
当然,ndarray它也可以处理 0 维数组,其中 0 表示它只是一个元素:
println!("\n{}", array![2.]);
println!("Dimensions: {}", array![2.].ndim());
正确输出如下:
[2]
Dimensions: 1
同样,我们也可以发展到3D或更高版本。
let arr12 = Array::<i8, _>::ones((2, 3, 2, 2));
println!("\nMULTIDIMENSIONAL\n{}", arr12);
猜到它的输出结果了吗?
MULTIDIMENSIONAL
[[[[1, 1],
[1, 1]],
[[1, 1],
[1, 1]],
[[1, 1],
[1, 1]]],
[[[1, 1],
[1, 1]],
[[1, 1],
[1, 1]],
[[1, 1],
[1, 1]]]]
这是一个包含 2 个元素的向量,重复 3 次,再重复 2 次;只需从右到左将其从小到大展开(反之亦然)。
如果还有不清楚的地方,别担心:我们更关注编程本身,而不是背后的数学/统计数据。
让我们给这团乱麻增添一些随机性吧!
我们还将其加载到前面简要介绍过的Cargo.tomlndarray-rand文件中。
该软件包将rand crate的功能(它将其重新导出为子模块)添加到您的ndarray 生态系统中。
为了查看一些示例,让我们在src/main.rs 文件use的相应部分添加以下内容。
use ndarray_rand::{RandomExt, SamplingStrategy};
use ndarray_rand::rand_distr::Uniform;
然后我们可以得到一个形状为 的数组(5, 2),例如,其中填充了介于 1 和 10 之间的均匀分布值(虽然是浮点数):
let arr13 = Array::random((2, 5), Uniform::new(0., 10.));
println!("{:5.2}", arr13);
例如,其结果为:
[[ 2.04, 0.15, 6.66, 3.06, 0.91],
[ 8.18, 6.08, 6.99, 4.45, 5.27]]
每次运行的结果应该有所不同,因为分布是(伪)随机的。
我们还可以通过以下方式从数组中“选取”数据(采样):
let arr14 = array![1., 2., 3., 4., 5., 6.];
let arr15 = arr14.sample_axis(Axis(0), 2, SamplingStrategy::WithoutReplacement);
println!("\nSampling from:\t{}\nTwo elements:\t{}", arr14, arr15);
这可能导致:
Sampling from: [1, 2, 3, 4, 5, 6]
Two elements: [4, 2]
让我展示另一种采样方法,这种方法需要使用 craterand并从向量创建一个数组:
首先,我们需要在该部分添加以下内容use:
use ndarray_rand::rand as rand;
use rand::seq::IteratorRandom;
因此,我们使用rand重新导出的 crate ndarray-rand。
然后我们可以执行以下操作(示例来自rand 文档,已进行改编):
let mut rng = rand::thread_rng();
let faces = "😀😎😐😕😠😢";
let arr16 = Array::from_shape_vec((2, 2), faces.chars().choose_multiple(&mut rng, 4)).unwrap();
println!("\nSampling from:\t{}", faces);
println!("Elements:\n{}", arr16);
我们thread_rng首先定义要使用的表情符号,然后设置一个包含我们要选择的表情符号的字符串。
然后我们从向量创建一个数组,并赋予其特定形状。我们选择的形状是(2, 2),但向量是使用特定的方法创建的IteratorRandom,即choose_multiple从字符串中随机提取 4 个元素(字符)。
结果显而易见:
Sampling from: 😀😎😐😕😠😢
Elements:
[[😀, 😎],
[😢, 😠]]
但要注意不要过度采样,否则choose_multiple会引发 panic。
相反,Array::from_shape_vec它会返回一个Result结果,说明是否可以创建一个数组(我们只需解包该结果即可)。
咱们来做一些统计,并把一些东西可视化一下,好吗?
在介绍可视化之前,让我们先介绍一下ndarray-stats这个 crate ,实际上,还要介绍一下noisy_float这个 crate ,在使用时它是必须的ndarray-stats。
首先,我们从随机创建的标准正态分布开始。
首先我们添加:
use ndarray_rand::rand_distr::{Uniform, StandardNormal};
那么,就让它放在它应该在的地方吧:
let arr17 = Array::<f64, _>::random_using((10000,2), StandardNormal, &mut rand::thread_rng());
这样我们就得到了一个包含 10,000 对元素的二维数组
use然后,我们再将进行统计分析所需的导入项添加到该部分:
use ndarray_stats::HistogramExt;
use ndarray_stats::histogram::{strategies::Sqrt, GridBuilder};
use noisy_float::types::{N64, n64};
现在我们需要将每个元素从浮点数转换为带噪声的浮点数;我不会解释带噪声的浮点数,只需将其视为不会静默失败的浮点数(成为NaN);此外,这样它就可以排序,这是ndarray-stats创建直方图所需要的。
为了对 ndarray 的每个元素按值执行操作,我们将使用mapv()类似于map()迭代器标准的函数。
let data = arr17.mapv(|e| n64(e));
此时,我们可以为直方图创建一个网格(需要网格将数据分成若干组);我们尝试推断出最佳方法,使用strategies::Sqrt(许多程序,包括 MS Excel,都使用的一种策略):
let grid = GridBuilder::<Sqrt<N64>>::from_array(&data).unwrap().build();
现在我们有了网格,也就是一种划分原始数据以准备直方图的方法,我们就可以创建这样的直方图了:
let histogram = data.histogram(grid);
为了得到底层计数矩阵,我们可以简单地这样表述:
let histogram_matrix = histogram.counts();
计数矩阵只是说明网格中每个箱子和每个高度中存在多少个元素。
好了,现在我们有了直方图……但是我们该如何将其可视化呢?
嗯,在可视化数据之前,我们应该先对数据进行一些准备工作。
我们面临的问题是,我们拥有网格的计数,但要绘制它,我们实际上应该有箱的数量以及该箱中的所有元素,这意味着我们应该垂直对所有元素求和。
为此,我们需要对 ndarray 的 axis(0) 进行求和:
let data = histogram_matrix.sum_axis(Axis(0));
现在我们得到了一个包含网格所有总和的一维 ndarray。此时我们可以确定每个总和对应一个不同的 bin,并逐一枚举它们。为了便于可视化工具使用,我们将所有数据转换为元组向量,其中元组的第一个元素是 bin 的编号,第二个元素是 bin 的高度。
let his_data: Vec<(f32, f32)> = data.iter().enumerate().map(|(e, i)| (e as f32, *i as f32) ).collect();
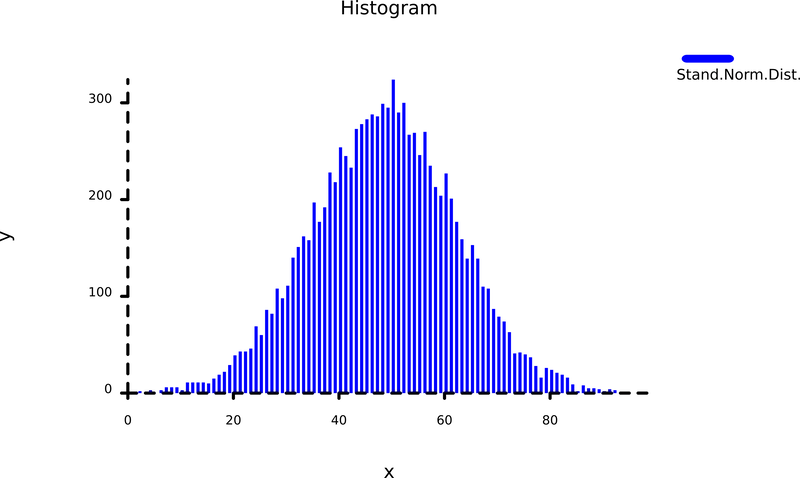
请记住:这只是一个虚假数据集,基于伪随机数生成器生成的正态分布(即中心位于0.0,半径约为的正态分布1)。尽管如此,我们应该能在直方图上看到一个大致呈正态分布的形状。
数据可视化
为了将事物可视化,我们将使用poloto,它是 Rust 中众多绘图库之一。
这是一个很简单的程序,也就是说我们不需要很多代码就能在屏幕上显示一些东西。
由于它非常简单,我们不会在本use部分中导入它。下面我将分三步解释如何绘制直方图:
第一步——创建一个文件来存储我们的图表:
let file = std::fs::File::create("standard_normal_hist.svg").unwrap();
第二步——根据数据创建直方图:
let mut graph = poloto::plot("Histogram", "x", "y");
graph.histogram("Stand.Norm.Dist.", his_data).xmarker(0).ymarker(0);
我们创建一个Plotter对象,为其指定标题和每个轴的图例。
然后,我们在该对象上绘制直方图,并将标题赋值给图例("Stand.Norm.Dist.")。
第三步——将图表写入磁盘:
graph.simple_theme(poloto::upgrade_write(file));
就这么简单!
让我们来欣赏一下我们(随意创作的)艺术作品:
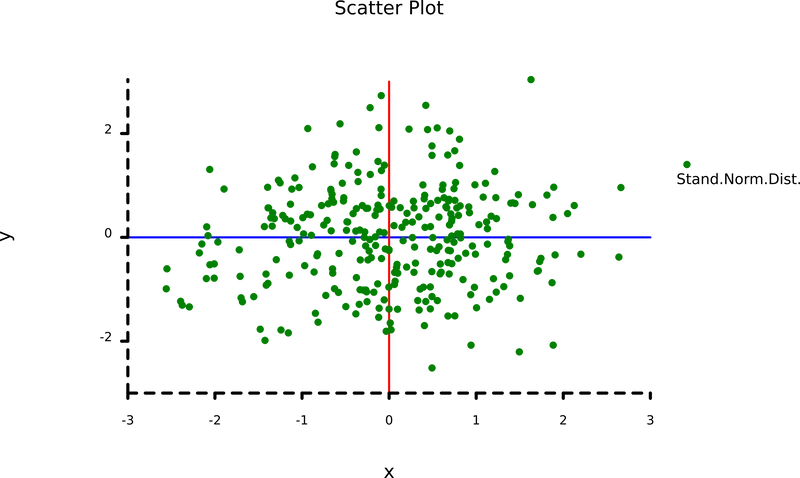
好的,我们换个方法:把图表看作散点图。由于我们的虚假数据服从标准正态分布,如果有 N 对坐标,那么散点图应该像一个以这些0,0坐标为中心的云状区域。
让我们把它形象化!
let arr18 = Array::<f64, _>::random_using((300, 2), StandardNormal, &mut rand::thread_rng());
let data: Vec<(f64, f64)> = arr18.axis_iter(Axis(0)).map(|e| {
let v = e.to_vec();
(v[0], v[1])
}).collect();
(0, 0)我们根据标准正态分布,创建了 300 对以 为中心的随机数。
然后我们将该数组转换为Vec<(f64, f64)>,因为该poloto库只能将图[f64; 2]或其他任何内容转换为AsF64。
我们还会添加两条线来表示图表的中心:
let x_line = [[-3,0], [3,0]];
let y_line = [[0,-3], [0, 3]];
接下来,我们创建一个文件,绘制图形,然后保存,就像我们之前绘制直方图一样:
let file = std::fs::File::create("standard_normal_scatter.svg").unwrap(); // create file on disk
let mut graph = poloto::plot("Scatter Plot", "x", "y"); // create graph
graph.line("", &x_line);
graph.line("", &y_line);
graph.scatter("Stand.Norm.Dist.", data).ymarker(0);
graph.simple_theme(poloto::upgrade_write(file));
就这样!现在我们可以欣赏我们随意创作的作品了:
结论
我想今天就到此为止吧。
我们看到了如何使用ndarray(基本形式),以及它与 Rust 数组和向量有何不同。
我们还看到了一些配套的模块,它们完善了整个生态系统,提供了随机性和一些统计功能。
此外,我们还了解了一种用数据绘制图表的方法,展示了如何绘制直方图、散点图和一些折线图。
我希望这将是一个良好的开端,让我们能够更深入地探索 Rust 在数据科学中的应用。
今天就到这里啦,下次再见!
文章来源:https://dev.to/davidedelpapa/rust-for-data-science-tutorial-1-4g5j