使用 Python 将吉他和弦巧妙地转换为钢琴乐谱

由 Mux 赞助的 DEV 全球展示挑战赛：展示你的项目！

— 嘿，你会弹奏歌曲 X 吗？

只是一个素不相识的朋友在你举办的派对上随便问了个问题。但如果你像我一样，小时候学过钢琴，现在偶尔还会弹弹乐玩玩，听到这种问题可能会很痛苦。问题是，我完全不会凭耳朵听音识谱，所以唯一能弹奏的办法就是找到乐谱。因此，我的第一步就是去谷歌搜索“ X乐谱pdf”或者“ X声乐谱pdf”，具体取决于X是什么。不幸的是，你经常会遇到以下问题：

钢琴谱存在，但其中只包含旋律本身以及一些非常有限的伴奏。
钢琴谱是存在的，但是需要付费才能获取。
根本没有钢琴版本。

你把调查结果告诉了邀请你一起玩X游戏的朋友，他/她说：

— 哦，真可惜我没带吉他，我会弹和弦，只是我不会弹钢琴……

此时你可能会想：啊，我很久以前学过一点乐理知识，只要读出和弦的名称，在钢琴上弹奏和弦应该不会太难吧？或者……真的那么难吗？

事实证明，如果你以前没做过，这实际上比视奏乐谱要难得多。你需要提前思考，在脑海中解码和弦（如果遇到一些不熟悉的复杂和弦记谱方式，难度会更大），并找到一种合理的双手演奏方法。我可以向你保证，你会发现自己的双手在键盘上移动得相当混乱。的确，和弦进行中，这一点并不那么显而易见。 $\mathrm{D_m\,F\,A_m}$ 你只需将一个手指向右移动一个全音或半音，而不必将整只手（或者更确切地说，两只手）向右移动小三度或大三度。

这时我才意识到，我终究是个软件工程师，而不是音乐家。所以，我决定放弃练习，直接写个脚本来简化我的工作。

本文余下部分分为四个部分：

在 Python 中处理吉他和弦
生成钢琴乐谱
优化钢琴和弦表示
将所有部件组装在一起

我选择 Python 作为编程语言，原因正如你可能猜到的那样，Python 中有大量的音乐处理库。我发现 Music21mingus是处理吉他和弦和music21生成钢琴谱最简单的库。虽然 Music21 功能非常强大，可能也能完成所有工作，但我发现将这两个库结合起来使用比用 Music21 实现我需要的 Mingus 功能要容易得多。

总之，您将在下面看到的大部分代码都是使用 Google Colaboratory 作为 IDE 编写的，您可以在文章末尾找到它的链接。

使用吉他和弦

正如人们常说的，条条大路通罗马。同样，大多数和弦在吉他上都有多种表示方法，尽管大多数业余吉他手通常只会使用每种和弦的单一表示方法。mingus它有一个很棒的功能，可以生成所有合理的和弦演奏方法：

from mingus.extra.tunings import get_tuning
from mingus.containers import NoteContainer, Note

guitar_tuning = get_tuning('guitar', 'standard')

guitar_tuning.find_chord_fingering(NoteContainer().from_chord('Dbm6'))

输出：[[0, 1, 2, 1, 2, 0], ...]

[[0, 1, 2, 1, 2, 0],
 [0, 1, 2, 1, 2, 4],
 [6, 7, 6, 6, 9, 6],
 [6, 7, 8, 6, 9, 6],
 [6, 7, 6, 6, 9, 9],
 [9, 7, 6, 6, 9, 6],
 [9, 11, 11, 9, 11, 9],
 [12, 11, 11, 13, 11, 12],
 [0, 1, None, 1, 2, 0],
 [0, 1, 2, 1, 2, None],
 [0, 1, None, 1, 2, 4],
 [6, 7, 6, 6, None, 6],
 [6, 7, 6, 6, 9, None],
 [6, 7, 6, 6, None, 9],
 [6, 7, None, 6, 9, 6],
 [9, 7, 6, 6, None, 6],
 [None, 7, 6, 6, 9, 6],
 [9, 11, None, 9, 11, 9],
 [12, 11, 11, None, 11, 12],
 [12, 11, 11, 13, 11, None],
 [None, 11, 11, 13, 11, 12],
 [0, 1, None, 1, 2, None],
 [6, 7, 6, 6, None, None],
 [None, 7, 6, 6, None, 6],
 [12, 11, 11, None, 11, None],
 [None, 11, 11, None, 11, 12]]

这里的数字对应于吉他指板上每根琴弦的位置。要获得每个手指对应的实际音高，我们可以使用guitar_tuning.get_Note：

for fingering in guitar_tuning.find_chord_fingering(NoteContainer().from_chord('Dbm6')):
  chord_pitches = [ guitar_tuning.get_Note(string=i, fret=fingering[i]) if fingering[i] is not None else None for i in range(6) ]
  print(chord_pitches)

['E-2'、'A#-2'、'E-3'、'G#-3'、'C#-4'、'E-4'] ...

['E-2', 'A#-2', 'E-3', 'G#-3', 'C#-4', 'E-4']
['E-2', 'A#-2', 'E-3', 'G#-3', 'C#-4', 'G#-4']
['A#-2', 'E-3', 'G#-3', 'C#-4', 'G#-4', 'A#-4']
['A#-2', 'E-3', 'A#-3', 'C#-4', 'G#-4', 'A#-4']
['A#-2', 'E-3', 'G#-3', 'C#-4', 'G#-4', 'C#-5']
['C#-3', 'E-3', 'G#-3', 'C#-4', 'G#-4', 'A#-4']
['C#-3', 'G#-3', 'C#-4', 'E-4', 'A#-4', 'C#-5']
['E-3', 'G#-3', 'C#-4', 'G#-4', 'A#-4', 'E-5']
['E-2', 'A#-2', None, 'G#-3', 'C#-4', 'E-4']
['E-2', 'A#-2', 'E-3', 'G#-3', 'C#-4', None]
['E-2', 'A#-2', None, 'G#-3', 'C#-4', 'G#-4']
['A#-2', 'E-3', 'G#-3', 'C#-4', None, 'A#-4']
['A#-2', 'E-3', 'G#-3', 'C#-4', 'G#-4', None]
['A#-2', 'E-3', 'G#-3', 'C#-4', None, 'C#-5']
['A#-2', 'E-3', None, 'C#-4', 'G#-4', 'A#-4']
['C#-3', 'E-3', 'G#-3', 'C#-4', None, 'A#-4']
[None, 'E-3', 'G#-3', 'C#-4', 'G#-4', 'A#-4']
['C#-3', 'G#-3', None, 'E-4', 'A#-4', 'C#-5']
['E-3', 'G#-3', 'C#-4', None, 'A#-4', 'E-5']
['E-3', 'G#-3', 'C#-4', 'G#-4', 'A#-4', None]
[None, 'G#-3', 'C#-4', 'G#-4', 'A#-4', 'E-5']
['E-2', 'A#-2', None, 'G#-3', 'C#-4', None]
['A#-2', 'E-3', 'G#-3', 'C#-4', None, None]
[None, 'E-3', 'G#-3', 'C#-4', None, 'A#-4']
['E-3', 'G#-3', 'C#-4', None, 'A#-4', None]
[None, 'G#-3', 'C#-4', None, 'A#-4', 'E-5']

请注意，黑键音符（或者更准确地说，与钢琴键盘上的黑键对应的音符）现在总是带有一个 $\锋利的$ ，从不与 $\平坦的$ . 的笔记 $\mathrm{D♭m6}$ 和弦在技术上应该由以下部分组成： $\mathrm{D\flat, F\flat, A\flat, B\flat\kern-1.4pt\flat}$ ，而 $\mathrm{C\尖锐，E，G\尖锐，A\尖锐}$ 指的是 $\mathrm{C\sharp m6}$ 。这对吉他来说影响不大——毕竟音高相同，但对钢琴乐谱来说就重要多了，因为和弦必须与当前的调号相匹配。我将在下一节中讲解如何解决这个问题。

生成钢琴乐谱

为了处理钢琴乐谱，我将使用库music21。

以下是手动生成钢琴乐谱的最基本方法：

import music21 as m21
sc1 = m21.stream.Score()
right_hand = m21.stream.PartStaff()
left_hand = m21.stream.PartStaff()
right_hand.append(m21.key.Key('Ab', 'major'))
right_hand.append(m21.note.Note('D-4'))
right_hand.append(m21.note.Note('F-4'))
right_hand.append(m21.note.Note('A-4'))
right_hand.append(m21.note.Note('B--4'))
left_hand.append(m21.chord.Chord(
    [m21.note.Note('D-3'), m21.note.Note('A-3')],
    duration=m21.duration.Duration(4)))
sc1.insert(0, right_hand)
sc1.insert(0, left_hand)
sc1.insert(0, m21.layout.StaffGroup([right_hand, left_hand], symbol='brace'))

sc1.show()

你已经可以注意到它们在表示音符的方式上music21存在一些差异：mingus

music21用途#或-变更标记；
mingus使用#和b，而-只是音符和八度之间的分隔符。

如果您尝试简单地按名称将一个库中的音符映射到另一个库，这可能会产生奇怪的效果：

mingus_note = Note('A-6')
print(mingus_note.to_hertz())
print(m21.pitch.Pitch(str(mingus_note).strip("'")).freq440)  # BAD!
print(m21.pitch.Pitch(mingus_note.name, octave=mingus_note.octave).freq440) # GOOD
print()

# Music21 can parse flats at the input (bemols)
mingus_note = Note('Db-5')
print(mingus_note.to_hertz())
print(m21.pitch.Pitch(mingus_note.name, octave=mingus_note.octave).freq440)
print()

# ... but not double-flats.
mingus_note = Note('Dbb-5')
print(mingus_note.to_hertz())
try:
  print(m21.pitch.Pitch(mingus_note.name, octave=mingus_note.octave).freq440)
except Exception as e:
  print(e)

上述代码块的输出结果为：

1760.0
1661.218790319782
1760.000000000002

554.3652619537442
554.3652619537443

523.2511306011972
bb is not a supported accidental type

现在让我们定义一些简单的语言来描述我们的和弦序列：每个和弦都将表示为duration:chord_symbol，其中duration以四分音符（或四分音符）表示，并chord_symbol以吉他记谱法表示：

4:Am 4:H7 2:E 2:E7 8:Am 4:H7 2:E 2:E7 4:Am

你可能会对这里的H音感到困惑——是的，这首歌显然遵循了德国和弦记谱法的传统。德语和英语音符名称之间唯一的重要区别在于B和H：

英语	德语
$\mathrm{B}$	$\mathrm{H}$
$\mathrm{B\flat}$	$\mathrm{B}$

将德语转换成英语就非常简单了：

def de_germanize(chord_sym: str):
    if chord_sym.startswith('B'):
        return 'Bb' + chord_sym[1:]
    if chord_sym.startswith('H'):
        return 'B' + chord_sym[1:]
    return chord_sym

我们将这样做——采用第一种指法mingus，用左手弹奏下面的 3 根弦，用右手弹奏上面的 3 根弦。

代码

from typing import Tuple, Sequence, List, Optional, NamedTuple

def notes_from_fingering(fingering: Sequence[int]) -> Tuple[Optional[m21.pitch.Pitch]]:
  result = []
  for i, fret in enumerate(fingering):
    if fret is None:
      result.append(None)
      continue
    mingus_note = guitar_tuning.get_Note(string=i, fret=fret)
    # Here mingus_note.name be one of: C, C#, D, D#, E, F, F#, G, G#, A, A#, B.
    pitch = m21.pitch.Pitch(mingus_note.name, octave=mingus_note.octave)
    result.append(pitch)
  return tuple(result)


def chord_or_rest_from_notes(notes: Sequence[m21.pitch.Pitch], **kwargs) -> m21.note.GeneralNote:
  if notes:
    return m21.chord.Chord(notes=notes, **kwargs)
  else:
    return m21.note.Rest(**kwargs)


def get_harmony_symbol_from_name(chord_name):
  if chord_name[1:].startswith('b'):
      chord_name = chord_name[0:1] + '-' + chord_name[2:]
  return m21.harmony.ChordSymbol(figure=chord_name)


def init_score_and_hands() -> Tuple[m21.stream.Score, m21.stream.PartStaff, m21.stream.PartStaff]:
  score = m21.stream.Score()
  right_hand = m21.stream.PartStaff()
  left_hand = m21.stream.PartStaff()
  # Force treble clef in right hand and bass clef in left hand.
  right_hand.append(m21.clef.TrebleClef())
  left_hand.append(m21.clef.BassClef())
  score.insert(0, right_hand)
  score.insert(0, left_hand)
  score.insert(0, m21.layout.StaffGroup([right_hand, left_hand], symbol='brace'))
  return score, left_hand, right_hand


class ChordForTwoHands(NamedTuple):
  left_hand_notes: Tuple[m21.pitch.Pitch]
  right_hand_notes: Tuple[m21.pitch.Pitch]


def get_hands_from_notes(notes: Sequence[Optional[m21.pitch.Pitch]]) -> ChordForTwoHands:
  return ChordForTwoHands(
      left_hand_notes=tuple(n for n in notes[:3] if n is not None),
      right_hand_notes=tuple(n for n in notes[3:] if n is not None)
  )


def score_from_chords(chords_string):
  score, left_hand, right_hand = init_score_and_hands()
  for token in chords_string.split():
    dur, chord_symbol = token.split(':')
    duration = m21.duration.Duration(quarterLength=float(dur))
    chord_symbol = de_germanize(chord_symbol)
    mingus_chord = NoteContainer().from_chord(chord_symbol)
    fingerings = guitar_tuning.find_chord_fingering(mingus_chord)
    notes = notes_from_fingering(tuple(fingerings[0]))
    harmony = get_harmony_symbol_from_name(chord_symbol)
    right_hand.append(harmony)
    chord_2h = get_hands_from_notes(notes)
    right_hand.append(chord_or_rest_from_notes(chord_2h.right_hand_notes, duration=duration))
    left_hand.append(chord_or_rest_from_notes(chord_2h.left_hand_notes, duration=duration))
  return score

score_from_chords('2:Gm 2:A7 2:Dm 2:B 2:Gm 2:Gm6 2:A7 2:Dm').show()

正如预期的那样，在“和弦→指法→音高→和弦进行”的过程中，我们丢失了所有关于和弦正确变音记号的信息。在上面的例子中，你可以注意到这一点。 $\mathrm{B\flat}$ 表示为 $\mathrm{A\sharp}$ 。所以，让我们尝试通过将和弦中的音符改为有效的等音符来纠正错误：

代码

def find_enharmonic_from_list(pitch: m21.note.Pitch, allowed_note_names: Sequence[str]):
    if pitch.name in allowed_note_names:
        return pitch
    for enharmonic in pitch.getAllCommonEnharmonics():
        if enharmonic.name in allowed_note_names:
            return enharmonic
    assert(False)


def fix_enharmonisms(pitches: Sequence[Optional[m21.pitch.Pitch]], harmony: m21.harmony.ChordSymbol):
  allowed_note_names = [pitch.name for pitch in harmony.pitches]
  return tuple(
      pitch and find_enharmonic_from_list(pitch, allowed_note_names)
      for pitch in pitches
  )


def score_from_chords(chords_string):
  score, left_hand, right_hand = init_score_and_hands()
  for token in chords_string.split():
    dur, chord_symbol = token.split(':')
    duration = m21.duration.Duration(quarterLength=float(dur))
    chord_symbol = de_germanize(chord_symbol)
    mingus_chord = NoteContainer().from_chord(chord_symbol)
    fingerings = guitar_tuning.find_chord_fingering(mingus_chord)
    notes = notes_from_fingering(fingerings[0])    
    harmony = get_harmony_symbol_from_name(chord_symbol)
    right_hand.append(harmony)
    notes = fix_enharmonisms(notes, harmony)
    chord_2h = get_hands_from_notes(notes)
    right_hand.append(chord_or_rest_from_notes(chord_2h.right_hand_notes, duration=duration))
    left_hand.append(chord_or_rest_from_notes(chord_2h.left_hand_notes, duration=duration))
  return score

score_from_chords('2:Gm 2:A7 2:Dm 2:B 2:Gm 2:Gm6 2:A7 2:Dm').show()

这样好多了，但我们仍然无法控制拍号——它是 $\mathrm{\frac{4}{4}}$ 默认情况下，或者说密钥签名——它是 $C$ （或者更确切地说， $Am$ 如上例所示）。为了解决这个问题，我们将允许向两个谱表添加任意TinyNotation元素。由于 TinyNotation 不支持调号变化，我们将扩展其功能。

新的解析器将支持如下的分数描述：

[kDm 3/4] 2:F 1:Gm 1:Am 2:AmM7 6:Dm

另外，趁此机会，我们也把解析和渲染分开，因为稍后我们会在它们之间进行优化：

更多代码

import re
import functools
import copy

class KeyToken(m21.tinyNotation.Token):
    def parse(self, parent):
        keyName = self.token
        return m21.key.Key(keyName)


class BaseElement:
  def add_to_score(self, score: m21.stream.Score): ...


@functools.cache
def get_harmony_and_implementations(chord_symbol: str):
  harmony = get_harmony_symbol_from_name(chord_symbol)
  mingus_chord = NoteContainer().from_chord(chord_symbol)
  return harmony, tuple(
      get_hands_from_notes(
          fix_enharmonisms(
              notes_from_fingering(fingering),
              harmony
          ),
      )
      for fingering in guitar_tuning.find_chord_fingering(mingus_chord)
  )


class ChordElement(BaseElement):

  def __init__(self, token: str):
    duration, chord_symbol = token.split(':')
    self.duration = m21.duration.Duration(quarterLength=float(duration))
    chord_symbol = de_germanize(chord_symbol)
    self.harmony, self.implementations = get_harmony_and_implementations(chord_symbol)
    self.best_implementation_index = 0

  def add_to_score(self, score: m21.stream.Score):
    chord_2h = self.implementations[self.best_implementation_index]
    right_hand, left_hand = score.parts
    right_hand.append(copy.deepcopy(self.harmony))  # Copy to prevent "object already added"
    right_hand.append(chord_or_rest_from_notes(chord_2h.right_hand_notes, duration=self.duration))
    left_hand.append(chord_or_rest_from_notes(chord_2h.left_hand_notes, duration=self.duration))


class MetadataElement(BaseElement):
  def __init__(self, title: str):
    self.metadata = m21.metadata.Metadata(title=title)

  def add_to_score(self, score: m21.stream.Score):
    score.insert(0, self.metadata)


class RemarkElement(BaseElement):
  def __init__(self, text: str):
    self.expression = m21.expressions.TextExpression(text)
    self.expression.placement = 'above'

  def add_to_score(self, score: m21.stream.Score):
    score.parts[0].append(self.expression)


class TinyNotationElement(BaseElement):
  def __init__(self, token: str):
    assert(token[0] == '[' and token[-1] == ']')
    tnc = m21.tinyNotation.Converter(makeNotation=False)
    tnc.tokenMap.append((r'k(.*)', KeyToken))
    tnc.load(token[1:-1])
    tnc.parse()
    self.stream = tnc.stream

  def add_to_score(self, score: m21.stream.Score):
    for sub_element in self.stream:
      for part in score.parts:
        part.append(sub_element)


def parse_chords(chords_string: str) -> List[BaseElement]:
  result = []
  PATTERNS = (
      ('TINY', r'\[[^\]]+\]'),
      ('TITLE', r'TITLE\[(?P<TITLE_TEXT>[^\]]+)\]'),
      ('REMARK', r'REMARK\[(?P<REMARK_TEXT>[^\]]+)\]'),
      ('CHORD', r'\d+(\.\d*)?:\S+'),
      ('SPACE', r'\s+'),
      ('ERROR', r'.')
  )
  full_regex = '|'.join(f'(?P<{kind}>{expression})' for kind, expression in PATTERNS)
  for mo in re.finditer(full_regex, chords_string):
    token = mo.group()
    kind = mo.lastgroup
    if kind == 'TINY':
      result.append(TinyNotationElement(token))
    elif kind == 'TITLE':
      result.append(MetadataElement(mo.group('TITLE_TEXT')))
    elif kind == 'REMARK':
      result.append(RemarkElement(mo.group('REMARK_TEXT')))
    elif kind == 'CHORD':
      result.append(ChordElement(token))
    elif kind == 'SPACE':
      pass
    else: # Error
      raise RuntimeError(f'Unexpected token at position {mo.start()}: "{chords_string[mo.start():]}"')
  return result

def score_from_chords(chords_string: str):
  elements = parse_chords(chords_string)

  score, _, _ = init_score_and_hands()
  for element in elements:
    element.add_to_score(score)
  return score

score_from_chords('TITLE[Song of a page] [kDm 3/4] 2:F 1:Gm 1:Am 2:AmM7 REMARK[Arpeggios] 6:Dm').show()

优化钢琴和弦表示

为了选择最佳和弦序列，我们将使用以下模型：

每个和弦实现都会有其对应的计算难度。
乐谱中两个连续和弦之间的过渡也会计算出难度。

我们的目标是尽可能降低所有和弦和过渡的总难度。这可以通过动态规划方法或图上的最短路径搜索来实现。

总之，我们先从和弦难度入手，因为这样优化就变得很简单——只需从列表中选择最佳和弦即可：

描述和弦难度各个组成部分的代码

def chord_length_penalty(chord_2h: ChordForTwoHands) -> int:
  num_notes = len(chord_2h.left_hand_notes) + len(chord_2h.right_hand_notes)
  # Prefer chords with 5 notes across both hands and but force at least 3.
  return [400, 300, 200, 15, 5, 0, 2][num_notes]

def clef_mismatch_penalty(chord_2h: ChordForTwoHands) -> int:
  middle_c = m21.pitch.Pitch('C4')
  req_bars = 0
  if chord_2h.left_hand_notes:
    req_bars += max(chord_2h.left_hand_notes[-1].diatonicNoteNum - middle_c.diatonicNoteNum, 0)
  if chord_2h.right_hand_notes:
    req_bars += max(middle_c.diatonicNoteNum - chord_2h.right_hand_notes[0].diatonicNoteNum, 0)
  return req_bars * 3


def duplicate_note_penalty(chord_2h: ChordForTwoHands) -> int:
  all_notes = chord_2h.left_hand_notes + chord_2h.right_hand_notes
  # Make sure we don't attempt to put the same 
  if len(all_notes) != len(set(x.diatonicNoteNum for x in all_notes)):
    return 100
  return 0


def is_white_key(p: m21.pitch.Pitch) -> bool:
  return p.pitchClass not in (1, 3, 6, 8, 10)


def rakhmaninoff_penalty(pitches: Sequence[m21.pitch.Pitch]) -> int:
  if not pitches:
    return 0
  # Slightly penalize chords above one octave in span.
  if pitches[0].ps - pitches[-1].ps > 12.0:
    return 1
  else:
    return 0


def black_thumb_penalty(pitches: Sequence[m21.pitch.Pitch]) -> int:
  if len(pitches) < 2 or is_white_key(pitches[0]):
    return 0
  if len(pitches) == 2 and pitches[0].ps - pitches[1].ps <= 7.0:
    # Assume that up to pure fifth we can play the interval with other fingers.
    return 0
  else:
    return 4


def black_pinkie_penalty(pitches: Sequence[m21.pitch.Pitch]) -> int:
  # Penalize 5th finger on black keys when the middle key is white
  if len(pitches) < 3:
    # No middle key means many good options to play it.
    return 0
  if is_white_key(pitches[-1]) or not is_white_key(pitches[-2]):
    return 0
  return 6


def hand_penalty(pitches: Sequence[m21.pitch.Pitch]) -> int:
  return rakhmaninoff_penalty(pitches) + black_thumb_penalty(pitches) + black_pinkie_penalty(pitches)

# Since get_harmony_and_implementations is also cached,
# We will only compute difficulty per every chord implementation at most once.
@functools.cache
def chord_difficulty(chord_2h: ChordForTwoHands) -> float:
  return (
      hand_penalty(chord_2h.left_hand_notes) +
      hand_penalty(chord_2h.right_hand_notes[::-1]) +
      duplicate_note_penalty(chord_2h) +
      chord_length_penalty(chord_2h) +
      clef_mismatch_penalty(chord_2h)
  )


def optimize_chords(elements: Sequence[BaseElement]):
  for element in elements:
    if isinstance(element, ChordElement):
      difficulties = list(map(chord_difficulty, element.implementations))
      element.best_implementation_index = min(range(len(difficulties)), key=difficulties.__getitem__)


def score_from_chords(chords_string: str):
  elements = parse_chords(chords_string)
  optimize_chords(elements)

  score, _, _ = init_score_and_hands()
  for element in elements:
    element.add_to_score(score)
  return score

score_from_chords('2:Gm 2:A7 2:Dm 2:B 2:Gm 2:Gm6 2:A7 2:Dm').show()

现在我们来模拟双手在两个和弦之间移动的难度。我们假设两个和弦之间的距离等于它们对应音符之间距离的总和。显然，如果和弦的长度不同，这种方法就行不通了，所以我们将尝试使用动态规划来匹配一个和弦中的音符：

import numpy as np

def pitch_distance(first: m21.pitch.Pitch, second: m21.pitch.Pitch):
  return abs(int(first.ps) - int(second.ps))

def hand_distance(first: Sequence[m21.pitch.Pitch], second: Sequence[m21.pitch.Pitch]):
  if len(first) < len(second):
    first, second = second, first
  n = len(first)
  m = len(second)
  # m <= n
  ADD_REMOVE_PENALTY = 1
  d = np.ones((n + 1, m + 1), dtype=int) * 100000
  d[:, 0] = np.arange(n + 1) * ADD_REMOVE_PENALTY
  for i in range(1, n + 1):
    for j in range(1, m + 1):
      d[i, j] = min(
          d[i - 1, j] + ADD_REMOVE_PENALTY,
          d[i-1, j-1] + pitch_distance(first[i - 1], second[j - 1])
      )
  return d[n, m]

@functools.cache
def chord_distance(previous_chord_2h: ChordForTwoHands, current_chord_2h: ChordForTwoHands) -> int:
  return (
      hand_distance(previous_chord_2h.left_hand_notes, current_chord_2h.left_hand_notes) +
      hand_distance(previous_chord_2h.right_hand_notes, current_chord_2h.right_hand_notes)
  )

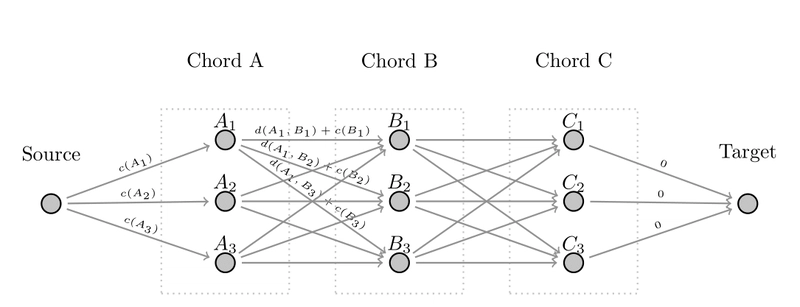
我们用表示单个和弦实现的复杂度（chord_difficulty） $c(X)$ 和两个和弦之间过渡的复杂性(chord_distance) $d(X, Y)$ 。令 $w(X, Y)$ 是 $c(Y) + d(X, Y)$ 。那么，用于优化和弦序列的图将如下所示：

现在，我们的优化问题就等价于在这个图中寻找最短路径。我在networkx这里使用了模块中实现的 Dijkstra 算法，但由于图的特性（它没有环，并且具有明显的拓扑有序性），如果您能找到更高效的方法，我不会感到惊讶。

代码

import networkx as nx

def optimize_chords(elements: Sequence[BaseElement]):
  graph = nx.DiGraph()
  graph.add_node('source')
  last_layer = ['source']

  for index, element in enumerate(elements):
    if isinstance(element, ChordElement):
      new_last_layer = []
      for impl_idx, impl in enumerate(element.implementations):
        n = f'{index}-{impl_idx}'
        graph.add_node(n, element=element, implementation_index=impl_idx, implementation=impl)
        for prev_node in last_layer:
          graph.add_edge(prev_node, n)
        new_last_layer.append(n)
      last_layer = new_last_layer

  graph.add_node('target')
  for n in last_layer:
    graph.add_edge(n, 'target')
  # Use weight function instead of explicit vertex/edge weights because
  # this will allow to perform difficulty/distance computation lazily.
  def weight_func(u, v, e):
    u_attr = graph.nodes[u]
    v_attr = graph.nodes[v]
    KEY = 'implementation'
    if KEY in v_attr:
      w = chord_difficulty(v_attr[KEY])
      if KEY in u_attr:
        w += chord_distance(u_attr[KEY], v_attr[KEY])
      return w
    else:
      return 0 
  path = nx.algorithms.dijkstra_path(graph, 'source', 'target', weight=weight_func)
  for node in path:
    attrs = graph.nodes[node]
    if 'element' in attrs:
      attrs['element'].best_implementation_index = attrs['implementation_index']

score_from_chords('2:Gm 2:A7 2:Dm 2:B 2:Gm 2:Gm6 2:A7 2:Dm').show()

将所有部件组装在一起

我们终于准备好用一首完整的歌曲来测试一下了：

score = score_from_chords("""
TITLE[Song of a page]
REMARK[transpose up by one tone (+2),
if the instrument supports it]

[kAm]

4:Am 4:H7 2:E 2:E7 8:Am
4:H7 2:E 2:E7 4:Am
2:Dm 2:G7 2:C 2:F 2:Dm 2:E7 4:Am
2:Gm 2:A7 2:Dm 2:B 2:Gm 2:Gm6 2:A7 2:Dm REMARK[(da capo)] [2/4] 2:Dm6
REMARK[(ending)] [4/4] 4:Gm 4:H7 4:E7 1:Am 1:E 2:Am
""").show()

完整的代码可以在这里找到，欢迎复制并尝试修改。

本文旨在验证概念。因此，这段代码无法适用于所有歌曲是完全可以理解的。以下是此原型中一些重要的缺失功能：

带有低音记谱法的和弦（例如 $E/A$ ）
休息
歌词
重复（这样整个优化问题就变得更难了）
调整和弦的长度以适应其持续时间

有些改动相对容易实现，而另一些改动（例如低音记谱法和重复）则需要更深层次的改变，甚至可能需要对整个方法进行彻底的重新设计。

不过，非常感谢您读到最后，如果我的文章能启发您编写一些音乐生成代码，或者哪怕只是让您掸去乐器上的灰尘，我都会非常高兴。

文章来源：https://dev.to/dlougach/a-smart-way-to-translate-guitar-chords-into-piano-sheet-music-with-python-22c2

菜单

分享

使用 Python DEV 的全球展示与讲述挑战赛（由 Mux 呈现）：巧妙地将吉他和弦转换为钢琴乐谱！

使用 Python 将吉他和弦巧妙地转换为钢琴乐谱

由 Mux 赞助的 DEV 全球展示挑战赛：展示你的项目！

使用吉他和弦

生成钢琴乐谱

优化钢琴和弦表示

将所有部件组装在一起

系统设计面试中的 19 种微服务模式

使用 React 和 AWS Amplify 实现无服务器架构第三部分：跟踪应用使用情况

模型-视图-控制器（MVC）模式到底是什么？DEV 全球项目展示挑战赛，由 Mux 主办：快来展示你的项目吧！

我在两年内从 PHP 开发人员晋升为高级 C#/.NET 开发人员。

了解 Docker：第 12 部分 – 传递构建参数

Yarn 和第三方 NPM 客户端的黑暗未来 DEV 的全球展示与讲述挑战赛，由 Mux 呈现：展示你的项目！

CSS DEV 的全球展示挑战赛“响应式字体”由 Mux 呈现：展示你的项目！

我是如何以学生开发者的身份免费获得 Tabnine Pro 的，你也可以！

五大顶级JS框架

从 Rector PHP 开始：利用自动化改进您的 PHP 代码