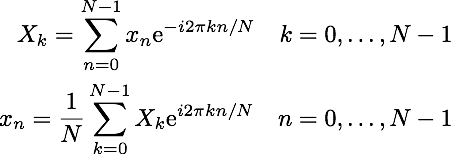在 JavaScript 中玩转离散傅里叶变换算法

太长不看

您可以在JavaScript 算法库中找到离散傅里叶变换算法。

离散傅里叶变换

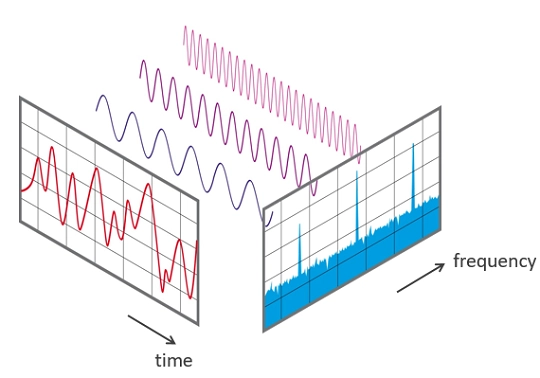
尽管离散傅里叶变换（DFT）可能不是你日常工作中会用到的算法，但它仍然是一种非常有趣的算法，值得研究。这并非因为它有多么复杂，而是因为它蕴含着深刻的意义。

该算法可以将时域分布的输入信号分解成若干个具有特定长度、振幅和相位的频率，使所有这些频率组合起来构成原始信号。因此，它实际上是将时间域转换为频率域，反之亦然。

这听起来可能很复杂，所以我们换个角度思考一下。

冰沙示例

想象一下，你有一杯奶昔。DFT 函数可以帮你把这杯奶昔分解成各种成分！想象一下，你把一瓶奶昔作为 DFT 函数的输入，它就能把它分解成三小瓶纯胡萝卜汁、苹果汁和橙汁！这就是 DFT 函数的工作原理——它将整个输入分解成各种成分。

油漆示例

或者想象一下，你想给栅栏刷漆，于是你混合了几种油漆，使它们颜色变得均匀。这时，DFT 函数就能将混合好的油漆分解成几种纯色，这些纯色混合在一起就能得到你最初想要的颜色！听起来是不是很神奇？

算法

算法的所有精妙之处和复杂性都隐藏在以下公式中：

你可以在JavaScript 算法库中找到这个公式的直接而简单的实现。这只是傅里叶变换的一个简单且效率不高（O(n^2)）的实现。但这些函数的目的仅仅是为了浅尝辄止地探索傅里叶变换这个复杂、深奥而又神奇的主题。

关于这个主题，有一篇非常好的文章。如果你有兴趣了解更多，我建议你读一读，因为里面有很多傅里叶变换的直观示例和交互式讲解。

希望你觉得傅里叶变换很有趣。祝你玩转算法！