运用德摩根定律和真值表理解逻辑和布尔代数
介绍
德摩根定律
真值表
用例
结论
参考
由 Mux 赞助的 DEV 全球展示挑战赛:展示你的项目!
介绍
借助德摩根定律和真值表,我们可以简化逻辑表达式和模型,发现可能性,甚至找出错误。这些方法帮助我们组织、简化,甚至可视化事物的工作原理。真值表在设计逻辑电路和逻辑门时也很有用。让我们深入了解一下。
德摩根定律
两个集合并集的补集是这两个集合的补集的交集,两个集合交集的补集是这两个集合的补集的并集。
我知道这听起来很晦涩难懂,但我个人通过这个例子理解了。
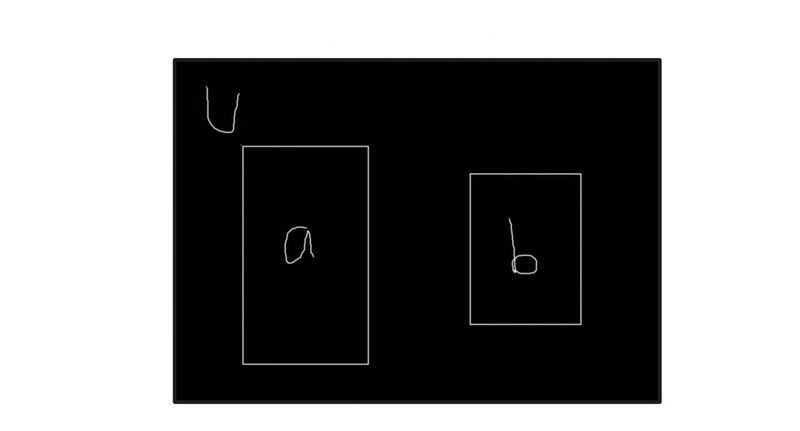
如果U为 {1,2,3,4,5,6},A为 {2,3},B为 {3,4,5}
//The union of A and B
A u B = {2,3,4,5}
// What the universal set contains and (A u B) doesn't
(A u B)' = {1,6}
// What the universal set contains and A doesn't
A' = {1,4,5,6}
//What the universal set contains and B doesn't
B' = {1,2,6}
//The intersection of the complements of A and B
A' n B' = {1,6}
A u B = A' n B'
在英语中,不可能同时是夏天和冬天,所以要么不是夏天,要么不是冬天。而既不是夏天也不是冬天,当且仅当它不是夏天或冬天。按照这个逻辑,AND 可以转化为 OR,反之亦然。
这基本上意味着
/*it cannot be summer and winter at once also
means it is either, not summer or not winter,
using the template that its either summer or winter that are available*/
!(Summer AND Winter) = !Summer OR !Winter
/*If its either not summer and not winter, that means it can't be summer or winter*/
!Summer AND !Winter = !(Summer OR Winter)
真值表
我们可以使用真值表来分析模型所依赖的内部变量。真值表的每一行代表变量的可能状态或组合。每个变量都有两种可能的结果,因此我们使用 2^n 公式,其中 n 是变量的数量。每个结果只能是真或假。
用例
class User {
constructor(firstname, lastname, isValidated, rateCount,isBlocked){
this.firstname = firstname;
this.lastname = lastname;
this.isValidated = isValidated;
this.rateCount = rateCount;
this.isBlocked = isBlocked;
}
writeToFile() {
if(!this.isBlocked && this.rateCount < 10 && this.isValidated ){
console.log('User is writing...');
this.addToRate();
}else console.log(`${this.firstname} ${this.lastname} you have issues`)
}
addToRate() {
this.rateCount ++;
}
get rate(){
return this.rateCount;
}
}
这是一个系统,它向已验证的用户授予写入权限,如果用户尝试使用未经验证的电子邮件地址向系统写入数据,或者在提交次数超过 10 次限制后尝试向系统写入数据,则会阻止该用户。
运用德摩根定律
我们想要分析导致用户被阻止的逻辑路径或过程。
A:未经验证的用户
B:向系统写入数据
C:超出速率限制(10)
D:用户被封禁
/*If an Unvalidated user writes to the system or if a validated user exceeds the limit, the user gets blocked.*/
(A AND B) OR (B AND C) -> D
//We can factorize using distributivity
B AND (A OR C) -> D
//The user remains unblocked at !D
!D -> !(B AND (A OR C)) // The law of contrapositivity
//Using DeMorgan's law (!(A AND B) = !A OR !B)
!D -> !B OR !(A OR C)
//Using DeMorgan's law again
!D -> !B OR (!A AND !C)
最后一个表达式告诉我们,如果用户不向系统写入数据,或者经过验证且未超过限制,则不会阻止该用户。
使用真值表
如果我们必须创建一个符合以下要求的系统
- 如果用户尚未验证其电子邮件,则其仅具有读取权限。
- 未经验证的用户不能拥有写入权限
- 用户拥有读取权限或写入权限。
A:未验证用户
B:读取权限
C:写入权限
- A ---> B(未验证用户只有读取权限)此语句仅在输出(B)为真或两者(A 和 B)都为假时才为真。
- !(A 和 C)(未经验证的用户不能拥有写入权限)
- B 或 C(用户要么拥有读取权限,要么拥有写入权限)
由于我们有三个变量,每个变量都有 8 种可能的结果(2^3),即真或假。然后,我们用上面三个陈述来检验这些可能的结果。
| 一个 | B | C | 1 | 2 | 3 | 全部的 |
|---|---|---|---|---|---|---|
| T | T | T | T | F | T | F |
| T | T | F | T | T | T | T |
| T | F | T | F | F | T | F |
| T | F | F | F | T | F | F |
| F | F | F | T | T | F | F |
| F | F | T | T | T | T | T |
| F | T | T | T | T | T | T |
| F | T | F | T | T | T | T |
所以我们可以看到,只有当至少一个变量为假或至少一个变量为真时,结果才会为真。它们不可能全部为假或全部为真。这很合理,你不可能在权限失效的情况下仍然需要写入权限。
结论
分析逻辑模型还有很多其他的规则和定律,这只是冰山一角。我偶然发现了它,觉得不错,所以决定分享给大家。感谢阅读!🌹🌹
原文发表于我的博客
参考
- 计算机科学精华作者:Wladston Ferreira Filho
- http://www.ask-math.com/de-morgans-law.html