使用堆在 Go 语言中实现 Dijkstra 算法
使用 Go 语言堆实现 Dijkstra 算法的简单方法。
由 Mux 赞助的 DEV 全球展示挑战赛:展示你的项目!
使用 Go 语言堆实现 Dijkstra 算法的简单方法。
什么是迪杰斯特拉?
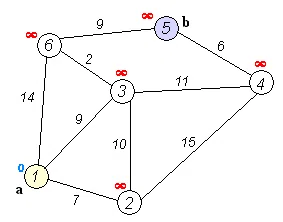
超简短描述:Dijkstra 算法用于查找 a 和 b 之间的最短路径。它选择距离最近的未访问节点,计算通过该节点到每个未访问邻居的距离,如果邻居的距离更小,则更新邻居的距离。
-
将所有节点标记为未访问节点。创建一个包含所有未访问节点的集合,称为未访问集;在本例中,我们将使用一个集合来存储已访问节点,而不是未访问节点。
-
为每个节点分配一个暂定距离值:初始节点的距离值设为零。将初始节点设为当前节点。
-
对于当前节点,考虑其所有未访问的邻居节点,并计算它们通过当前节点的暂定距离。将新计算的暂定距离与当前赋值进行比较,并赋值较小的值。例如,如果当前节点 A 的距离标记为 6,且连接 A 和邻居节点 B 的边的长度为 2,则 B 通过 A 的距离为 6 + 2 = 8。如果 B 之前被标记为大于 8 的距离,则将其更改为 8。否则,保持当前值不变。
-
当我们检查完当前节点的所有未访问邻居节点后,将当前节点标记为已访问。已访问的节点将不再被检查。
-
选择下一个未访问的节点,该节点的暂定距离最小,将其设置为新的“当前节点”,然后返回步骤 3。
什么是堆?
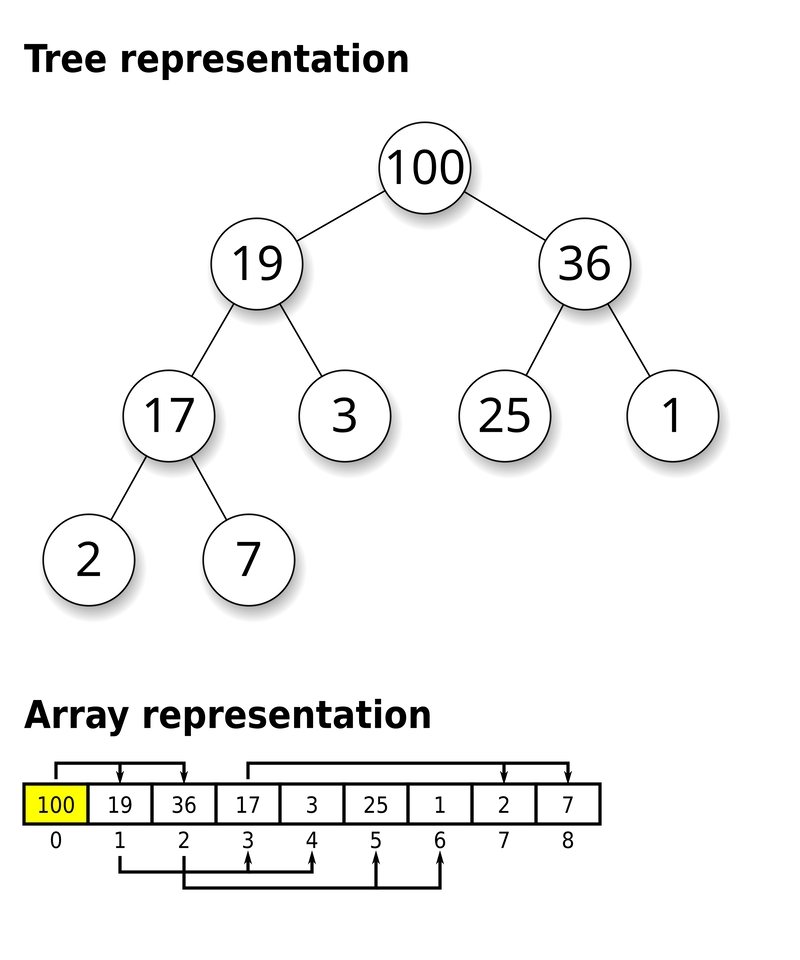
在计算机科学中,堆是一种特殊的基于树的数据结构,它本质上是一个几乎完全的树,满足堆的性质:在最大堆中,对于任意给定的节点 C,如果 P 是 C 的父节点,则 P 的键(值)大于或等于 C 的键。在最小堆中,P 的键小于或等于 C 的键。堆的“顶部”(没有父节点)的节点称为根节点。
堆可以被视为一个优先级队列;最重要的节点始终位于顶部,移除该节点后,替换它的节点将是最重要的。这在编写需要按完整顺序处理某些内容,但又不想执行完全排序或无需了解其余节点信息的算法时非常有用。例如,用于查找图中节点间最短距离的著名算法——Dijkstra 算法,可以通过使用优先级队列进行优化。
为什么?
我正在学习图论及其算法,因此我会在空闲时间阅读和学习这方面的知识。最近我观看了一个关于使用堆在 Python 中实现 Dijkstra 算法的视频,觉得很有趣,所以我决定用 Go 语言也实现同样的算法。
我知道有很多关于同一主题的文章,这些文章很好地解释了什么是 Dijkstra 算法或什么是堆,本文将是一篇简短的文章,只专注于实现,我想向你展示一个使用 Golang 中的堆来实现 Dijkstra 算法的非常简单的方法。
如果你想了解更多关于迪杰斯特拉的信息,你应该读读这篇文章,我发现它非常棒。
执行
Dijkstra 算法用于搜索两个节点之间的最短路径,它访问每个节点的邻居,计算成本和从起始节点出发的路径,并始终保持最小值。为此,我们可以使用最小堆在每次迭代中保存最小值,使用 push 和 pop 操作,这两个操作的时间复杂度均为 O(log n)。
首先,我们需要实现最小堆,golang 的标准库中有一个包可以实现这一点。
heap 包为任何实现了 heap.Interface 接口的类型提供堆操作。堆是一种树,其特性是每个节点都是其子树中值最小的节点。
堆.go
package main
import hp "container/heap"
type path struct {
value int
nodes []string
}
type minPath []path
func (h minPath) Len() int { return len(h) }
func (h minPath) Less(i, j int) bool { return h[i].value < h[j].value }
func (h minPath) Swap(i, j int) { h[i], h[j] = h[j], h[i] }
func (h *minPath) Push(x interface{}) {
*h = append(*h, x.(path))
}
func (h *minPath) Pop() interface{} {
old := *h
n := len(old)
x := old[n-1]
*h = old[0 : n-1]
return x
}
type heap struct {
values *minPath
}
func newHeap() *heap {
return &heap{values: &minPath{}}
}
func (h *heap) push(p path) {
hp.Push(h.values, p)
}
func (h *heap) pop() path {
i := hp.Pop(h.values)
return i.(path)
}
其次,我们需要实现图的逻辑,为此,我们使用一个结构体,其中包含一个映射来保存节点之间的边,以及用于添加边和从一个节点获取所有边的函数。
getPath 函数实现了 Dijkstra 算法,用于获取起点和终点之间的最短路径。
graph.go
package main
type edge struct {
node string
weight int
}
type graph struct {
nodes map[string][]edge
}
func newGraph() *graph {
return &graph{nodes: make(map[string][]edge)}
}
func (g *graph) addEdge(origin, destiny string, weight int) {
g.nodes[origin] = append(g.nodes[origin], edge{node: destiny, weight: weight})
g.nodes[destiny] = append(g.nodes[destiny], edge{node: origin, weight: weight})
}
func (g *graph) getEdges(node string) []edge {
return g.nodes[node]
}
func (g *graph) getPath(origin, destiny string) (int, []string) {
h := newHeap()
h.push(path{value: 0, nodes: []string{origin}})
visited := make(map[string]bool)
for len(*h.values) > 0 {
// Find the nearest yet to visit node
p := h.pop()
node := p.nodes[len(p.nodes)-1]
if visited[node] {
continue
}
if node == destiny {
return p.value, p.nodes
}
for _, e := range g.getEdges(node) {
if !visited[e.node] {
// We calculate the total spent so far plus the cost and the path of getting here
h.push(path{value: p.value + e.weight, nodes: append([]string{}, append(p.nodes, e.node)...)})
}
}
visited[node] = true
}
return 0, nil
}
main.go
package main
import (
"fmt"
)
func main() {
fmt.Println("Dijkstra")
// Example
graph := newGraph()
graph.addEdge("S", "B", 4)
graph.addEdge("S", "C", 2)
graph.addEdge("B", "C", 1)
graph.addEdge("B", "D", 5)
graph.addEdge("C", "D", 8)
graph.addEdge("C", "E", 10)
graph.addEdge("D", "E", 2)
graph.addEdge("D", "T", 6)
graph.addEdge("E", "T", 2)
fmt.Println(graph.getPath("S", "T"))
}
$ go run .
Dijkstra
12 [S C B D E T]