Java 中一个隐藏了近 9 年的漏洞终于被发现。

嗨，伙计们！😎

今天的故事有点特别，但肯定很有趣。我在Coursera上学习二叉搜索树的时候，教授讲了一个故事：2006年，Java二叉搜索实现使用9年后，发现了一个bug。这个bug只有在有人使用较大的int变量low和high的值时才会出现。让我来解释一下。

首先，也是最重要的事！🤓

什么是二叉搜索树？

根据维基百科的定义，二叉搜索树（BST）是

[...] 一种特殊的容器：一种在内存中存储“项”的数据结构。它们支持快速查找、添加和删除项，可用于实现动态项集或允许按键查找项的查找表。它们将键按排序顺序保存，以便查找和其他操作可以使用二分查找的原理：在树中查找键时，它们从根节点到叶节点遍历整棵树，将要查找的键与存储在树节点中的键进行比较，并根据比较结果决定继续在左子树还是右子树中查找。这意味着，平均每次比较操作都可以跳过大约一半的树。

好的，那我们能总结一下吗？当然可以！想象一棵树，树中的每个元素都已排序。要在树中查找元素，我们需要从根节点开始，检查目标元素是小于还是大于根节点。如果小于根节点，我们就向左查找；如果大于根节点，我们就向右查找。

我们以gif图中的例子为例。我们需要找到数字27；21是根，所以我们从这里开始。

27 大于或等于 21 吗？是的，所以向右走。
27 大于或等于 28 吗？不，所以向左走。
27 大于或等于 25 吗？不，所以向右走。
27 大于或等于 27 吗？是的，我们找到了答案！

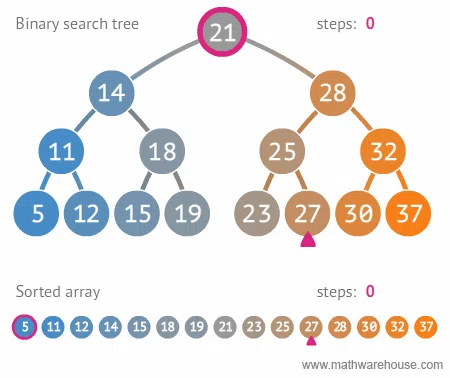
该 GIF 动画还展示了与已排序数组搜索的对比。我们可以看到，二叉搜索树的速度要快得多！

好的，现在我们来看看二叉搜索树的实现。

public static int binarySearch(int[] a, int key) {
    int low = 0;
    int high = a.length - 1;

    while (low <= high) {
        int mid = (low + high) / 2;
        int midVal = a[mid];

    if (midVal < key)
        low = mid + 1;
    else if (midVal > key)
        high = mid - 1;
    else
        return mid; // key found
    }
    return -(low + 1);  // key not found.
}

这是 Java 中的标准二分查找，它是用 java.util.Arrays 编写的。

从不同角度观察确实很难找到漏洞，这话没错，但也不完全对……好吧，让我解释一下……

虫子👨‍💻

错误出在这一行的数学细节上：

int mid =(low + high) / 2;

但为什么？

根据约书亚·布洛赫在他的文章中所述，

在《编程珠玑》一书中，Bentley 指出，类似的代码行“将 m 设置为 l 和 u 的平均值，并向下取整到最接近的整数”。乍一看，这个断言似乎是正确的，但当 int 变量 low 和 high 的值很大时，它就会失效。具体来说，如果 low 和 high 的和大于最大正整数值 (2³¹ - 1)，则此断言会失效。因为和会溢出为负值，并且除以 2 后结果仍然是负数。在 C 语言中，这会导致数组索引越界，并产生不可预测的结果。在 Java 中，它会抛出 ArrayIndexOutOfBoundsException 异常。

这种错误会在长度（以元素数量计）达到 2³⁰ 或更大（大约十亿个元素）的数组中出现。这在 20 世纪 80 年代《编程珠玑》出版时是不可想象的，但如今在谷歌和其他公司却很常见。在《编程珠玑》中，本特利写道：“虽然第一个二分查找算法发表于 1946 年，但第一个对所有n值都适用的二分查找算法直到 1962 年才出现。” 事实上，至少在主流编程语言中，真正正确的二分查找算法版本寥寥无几。