通过努力成为网球冠军来解释归并排序

归并排序是一种常用的数组排序算法，用于将数组元素从小到大进行排序。它经常被拿来与选择排序、插入排序、冒泡排序等算法进行比较。

然而，当我在网上搜索归并排序工作原理的简单解释时……我却找不到一个能将其解释得非常简单易懂的指南。

当然， VisuAlgo上有非常漂亮的图形可视化，FreeCodeCamp 也有全面的文字解释。

但是，我仍然会长时间盯着代码块，心想：“这一行到底发生了什么？”

所以，本指南将用极其简单易懂的方式解释归并排序的工作原理。它有点像一系列网球比赛。

要理解本指南，你只需要掌握递归的基础知识。让我们开始吧！

归并排序基础知识

与其他所有基本的 JavaScript 算法一样，归并排序的基本思想之一是，你只能通过一次比较两个元素并找到较大的元素来对数组进行排序。

因此，我们需要一种方法来尽可能高效地进行这些比较。

假设我们有一个包含 8 个数字的数组，我们需要将它们按从小到大的顺序排序：

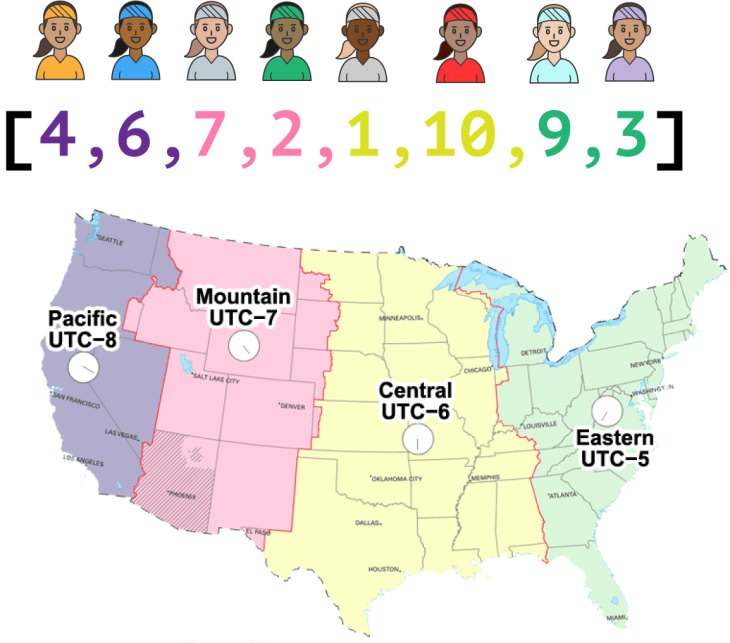
[4,6,7,2,1,10,9,3]

与其将这些视为数字，不如将它们视为网球运动员的技能水平，等级从 1 到 10。我们的任务是确定“这组人中谁是最好的网球运动员？”

因此，我们需要使用归并排序算法，将这组球员按技能水平从低到高进行排名。我们可以通过进行一系列网球比赛并确定每场比赛的获胜者来实现这一点。

但是，在真正的网球比赛中，球员们不必跨越全国参加一场大型锦标赛。相反，他们必须先赢得一系列小型锦标赛，才有资格争夺全国冠军的头衔。

假设我们要在美国寻找最好的业余球员。

我们可以将这些玩家分为四个区域：西部、山区、中部和东部。划分方式如下：

紫色数组中索引为 0 和 1 的元素位于西部地区……你应该明白我的意思了。

我们将首先举办 4 场区域锦标赛，然后让区域冠军之间进行比赛，以决出全国冠军。

换句话说，我们会不断选出两名网球选手中“更优秀”的那一位，直到达到国家级水平。到了国家级水平，“更优秀”的选手实际上就是全美“最优秀”的选手！

设置归并排序算法

好吧，我承认我选择8个玩家是因为这样在博客文章中更容易展示。为了使算法正常运行，它必须能够处理至少包含2个元素的所有数组。

而且，它还需要处理数组中元素个数为奇数的情况，例如 9 个元素。

归并排序实际上包含两个部分：

1. 将所有网球选手分成若干区域性锦标赛
2. 我们将逐步提高网球比赛的级别，直到决出全国冠军。

这就是为什么我们需要递归：在知道数组大小之前，我们无法确定需要运行多少场比赛。这个算法必须能够处理 8 位网球运动员……或者 350 位。

递归部分我们稍后再讲。现在，让我们重点关注第二部分，即“比较”函数，它允许我们比较两位网球运动员的水平，并根据他们的技能水平对他们进行排名。我们假设水平更高的运动员每次都会获胜。

该函数可以无限次运行，具体次数取决于玩家池的大小。

此函数应接收两个数组，并将它们合并成一个按从小到大排序的数组。它应该通过“比较”或一对一比较来实现这一点。

以下是两个各包含两个元素的数组的示例。这可能是区域赛结束后举行的锦标赛。

以下是关于上方GIF动画的几个关键说明：

1. 我们一次只能移动一个棋子。这是因为我们只能确定当前棋子是否比对手更强，而无法同时确定多个棋子的绝对位置。
2. 锦标赛的一侧可能聚集了所有最优秀的选手。因此，我们需要能够处理只剩下一侧选手的情况。

以下是代码：

const tournament = (left, right) => {
  var rankings = [];
  while(left.length || right.length) {
    if(left.length && right.length) {
      if(left[0] < right[0]) {
        rankings.push(left.shift())
      } else {
        rankings.push(right.shift())
      }
    } else if(left.length) {
        rankings.push(left.shift())
      } else {
        rankings.push(right.shift())
      }
    }
  return rankings;
}

一下子说了这么多，下面是概要：

1. 第 3 行：我们开始遍历对阵表两侧的球员。遍历次数由较长的数组决定。
2. 第 4-10 行：我们与每个数组中的第一个元素进行“竞争”。当找到失败者时，我们使用shift() 方法将该玩家从比赛中移除，并将其添加到排名数组中下一个最低的位置。
3. 最后一行：我们返回排名数组，其中玩家按排名从低到高排列。

以下是该代码的动画版本：

好的，现在让我们回到第一个函数，看看我们如何将选手分成区域级的锦标赛，然后再将他们组合成全国锦标赛。

在归并排序中使用递归

好了，我们现在有了可以运行“比赛”的函数，但是我们需要一个函数来拆分数组并将其重新组合起来。

在进行任何比赛之前，我们需要将数组组织成“区域”，然后才能进行第一次 1v1 比赛。

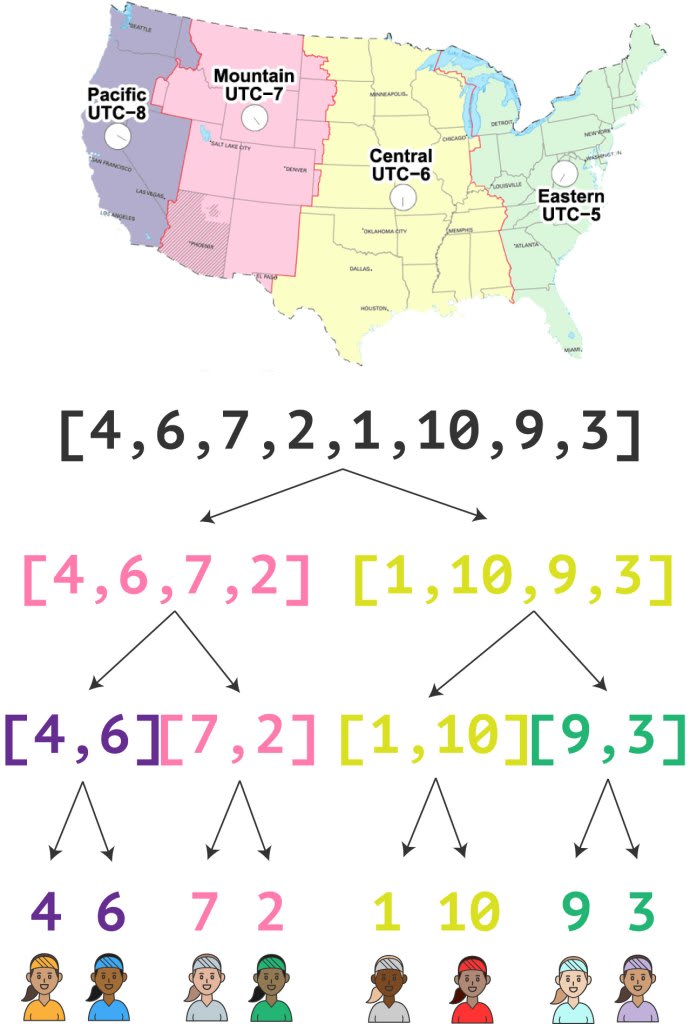
以下是如何将 8 名不同技能水平的玩家转化为 4 场 1 对 1 比赛的方法：

数组被拆分成更小的数组或单个元素的例子有 7 个。我们不能硬编码这个数字，因为如果有 16 个玩家，数组被拆分的例子就会有 15 个。

记住：在 1 对 1 的比较中，我们只能判断哪个玩家比另一个玩家“更强”。这就是为什么我们需要将其分解成 1 对 1 的比较——这样所有的小数组才能在后续比较之前正确排序。

然后，我们将对每一层的元素进行排序，并重新组装数组。

以下是比赛分组方式，分组将分为一系列 1 对 1 的比赛：

接下来，我们将“重新组装”数组，以找到从小到大的排名：

看出数组拆分和重组之间的相似之处了吗？这很好地提示我们需要用到递归。

我将重点关注数组的“左侧”，也就是前半部分。下面我们将介绍如何构建一个调用栈，以便对数组进行排序。

每次将数组一分为二时，我们都会在调用栈中添加一个引用前一次调用的函数。最后，我们可以对每一级数组运行 `tournament()` 函数，在合并它们之前对每个较小的数组进行排序。

以下是代码：

const findWinner = (players) => {
  if(players.length <= 1) return players;
  const middle = players.length / 2 ;
  const left = players.slice(0, middle);
  const right = players.slice(middle, players.length);
  return tournament(findWinner(left), findWinner(right));
}

let players = [4,6,7,2,1,10,9,3];
findWinner(players);

第 3-5 行允许我们定义数组的中点，并沿中点分割数组。递归地执行此操作，即可将数组缩小到只剩一个元素为止。

最重要的代码在第 2 行和第 6 行。

第 2 行处理数组缩减到只剩 1 个元素的情况。这表明递归应该停止，我们可以运行最低级别的区域性锦标赛。

在第 6 行，我们定义在每次调用中，我们将对上一次调用中排序后的数组运行 tournament() 函数（如果是最低级别，则运行 1v1 对决）。

这就是它的样子：

在上面的例子中，我们已经进入了“西部”和“山区”区域的 1v1 阶段。因此，我们可以从调用栈的顶部开始，多次调用 tournament() 函数，直到到达调用栈的末尾，从而找到排名第一的玩家。

获取最新教程

你喜欢这篇指南吗？在CodeAnalogies 博客上获取我最新的 HTML、CSS 和 JavaScript 主题的图文讲解。