对福特-约翰逊算法的人工解释和逐步可视化

福特-约翰逊排序算法，也称为归并插入排序，并非一种广为人知或流行的算法，其目标是尽可能减少元素间的比较次数。该算法鲜为人知的原因在于它既不快，也不是最优的最小排序算法，因此，无论是学术论文、晦涩难懂的计算机科学书籍，还是Reddit或Stack Overflow上一些零散的讨论帖，都鲜有关于该算法的优质资源。

这个算法与归并排序关系不大，但却经常被混淆。在 C++ 2009 的 42 学派中，为了简化算法，人们常常会犯一个错误，或者说是一种作弊手段，即实现一个介于归并排序和二分插入排序之间的混合排序算法。本文旨在通过简单的解释和对包含 22 个数字的数据集进行逐步演示，帮助读者理解该算法。

我叫埃尔达，是里昂42学院的一名学生。因此，这篇文章也与我的一项学校作业有关。我决定写一篇关于这个算法的文章，因为几乎没有人能正确且清晰地阐述这个算法，它难度很高，而且可以说是最复杂的排序算法之一。

算法步骤

我建议先阅读维基百科和克努特（Knuth）对该算法的描述。这两个来源对算法步骤的描述略有不同。我打算也给出自己的解释，因为我相信换一种方式表达有助于理解；之后我还会逐一深入解释每个步骤。因此，以下是我对使用该算法按升序对数字进行排序的步骤的解释：

1. 将数字递归地分成两两一组的数字，再分成两两一组的数字，如此循环往复，并按数字大小排序，直到无法再组成任何数字对为止。如果存在未配对的奇数元素，则保留它。
   • 我还会将我们操作的单位称为elements……elements可以是数字、数字对、数字对等等……
   • 我们将每对元素中的最小元素称为b，最大的元素称为a。根据元素对的索引，我们将它们称为b1，，，，a1... ，。b2a2bxax
2. 创建一个序列（在维基百科和克努特的书中分别称为序列S或the main chain序列），该序列由最小对中的最小元素（b1）和其余a元素组成。如果第一步正确完成，则该序列将已排序。创建一个由其余b元素（也称为序列the pend）以及奇数元素（如果有）组成的序列。
   • 从现在开始，我将把这些序列称为the main和。the pend
3. 将待插入元素按雅各布斯塔尔数顺序以二进制方式插入主元素。稍后我会解释其原理和工作方式。如果无法the main再使用雅各布斯塔尔数插入元素，则采用与传统二进制插入类似的方法，以相反的顺序插入元素。

由于步骤 1 是递归的，因此会产生多个递归层级，步骤 2 和 3 将应用于每一层级。其形式大致如下：

如果一切操作正确，序列就会排序成功。当然，为了概括描述我们将要进行的操作，我省略了一些细节。这个算法并不容易理解，也不指望你第一次阅读就能完全理解。在你看到使用既定术语的算法可视化图之后，你会对它有更清晰的认识。

第一步：分组和分类

这一步理解起来相当复杂，用代码实现起来也很棘手，但良好的可视化会有所帮助。难点在于，每次递归调用，我们处理的元素组都会越来越大：第一次调用处理一对数字，第二次调用处理一对对数字，第三次调用处理一对对对数字，以此类推，直到我们无法再将原始序列拆分成单个元素对为止。

除此之外，我们还需要保持原始的配对关系：我们不能在第五次递归调用中破坏第一次递归调用中形成的配对。这一点对于该算法至关重要，因为它依赖于元素的某些保证：集合 A 中的最大元素小于集合 B 中的最大元素，小于集合 Cb2中的最大元素a2，小于集合 D 中的最大元素，小于集合 E 中的最大元素，小于集合 C 中的最大元素。这对于算法的最小比较排序特性至关重要。实现这一点的最简单方法就是在排序时交换整组数字。稍后会更清楚。b3a3b4a4bxax

为了便于可视化，我会在顶部标出当前的递归深度。由于该算法需要在插入操作之前对键值对进行递归排序，我将在本节中演示这个过程。

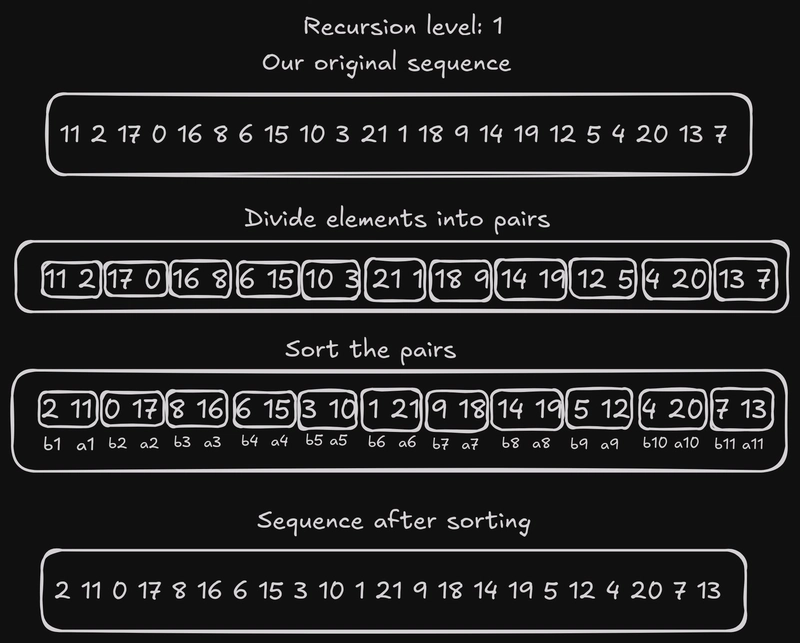
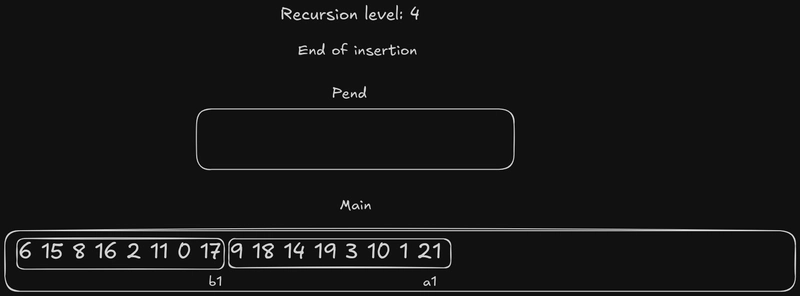
这种递归深度很容易理解：这里我们只处理数字。如果一对数字中一个大于另一个，我们就直接交换它们。排序完成后，我在新序列的每个元素下方添加了之前描述的b标签a：现在应该很清楚这些标签的作用了。

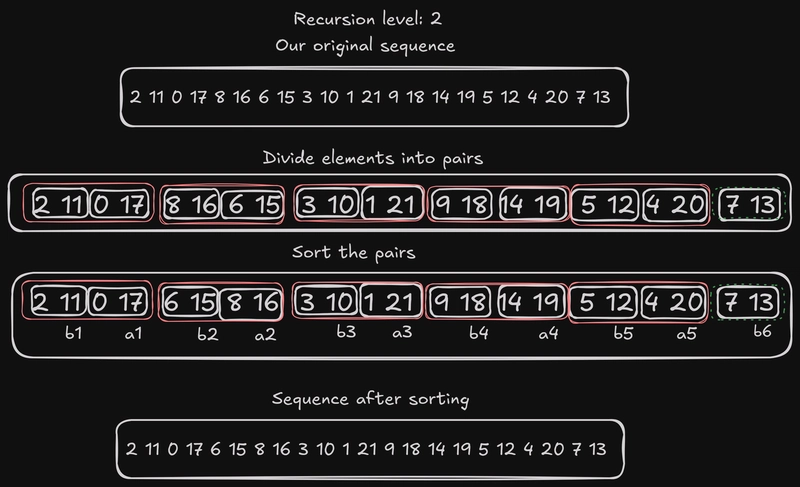
这里开始变得有点奇怪了：现在我们的元素不再只是一个数字，而是一对数字。此外，我们还有一个奇数元素，它没有对应的数字对。我们把它命名为b6。
在表示数字对的白色边框上方，还有红色边框表示数字对的两倍。还要注意的是，我把标签放在了每个元素的最后一个数字旁边：这并非巧合，标签位于我们实际用于比较/排序的数字下方：11例如，与 相对17，16与 相对15等等，但交换发生在整个数字子序列上。绿色虚线边框表示一个奇数对。这里只发生了一次交换： 和8 16的交换6 15。

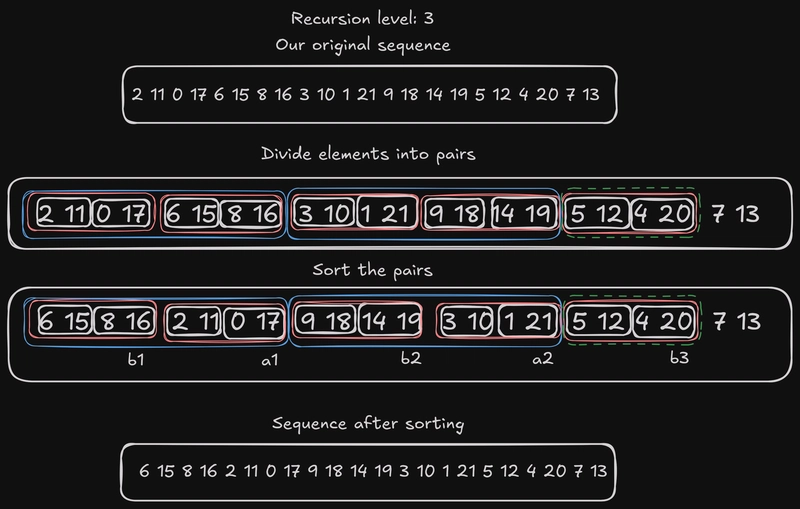
现在我们用蓝色边框来表示成对成对的数对……光是说起来就够绕口的了。但我们必须深入探究。
注意，有些数字没有边框：我选择这种方式来分隔那些甚至不能构成元素的数字。在这个层级，我们操作的最小单元由 4 个数字组成，而成对的数字则由 8 个数字组成。我们要如何处理这些数字呢？很简单：忽略它们。
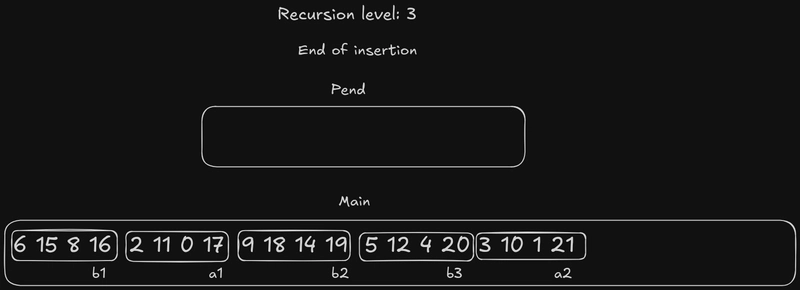
在这个层级，发生了两次交换：2 11 0 17和6 15 8 16，3 10 1 21以及9 18 14 19。

现在我们到了两两两的层级。我们有 22 个元素，但这里的元素是由 8 个数字组成的：因此只有一对两个元素。
17小于21。幸运的是！在这个层级没有发生交换。

递归到第 5 层时，已经无法继续进行下去：因为每次递归调用，元素中的数字数量都会翻倍，最终我们将无法组成一对元素。这就是我们从这一层跳出的原因。因为在第 5 层，一个元素包含 16 个数字，而总共只有 22 个数字，所以不可能组成一对两个元素。从现在开始，我们将从第 4 层开始，依次递归到第 3 层、第 2 层、第 1 层……直到得到排序后的数字序列。

为了真正理解排序过程中发生的现象，我建议你随机生成一个数字序列，然后在纸上尝试对它进行排序。练习几次之后，你或许就能想到如何在代码中实现这一步骤了。

步骤 2 和 3：初始化和插入

我们将一起讨论这两个步骤，因为算法的递归特性决定了它们会交替执行。步骤 1 独立运行，生成了 4 个递归层级，步骤 2 和步骤 3 需要处理这些层级。这些步骤会应用于每个层级。

这里我们之前定义的标签就派上用场了。
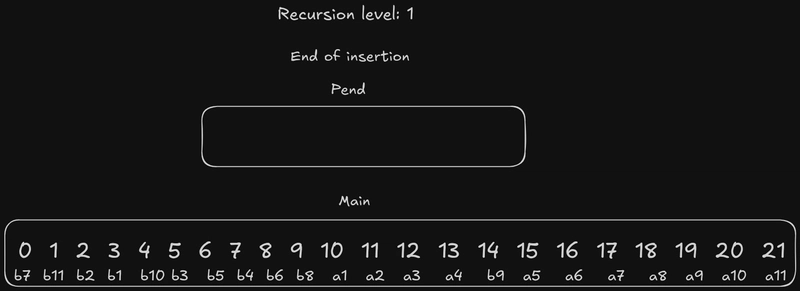
这一步很简单：
The main首先用元素初始化{b1, a1}，然后用剩余的a元素初始化。
The pend接着用剩余的b元素初始化，从开始b2。
The main此时应该已经排序了，但还没有完全排序。就像第一步的比较和交换一样，每个元素中只有最大的数字才算“排序完成”。让我们用已有的例子来演示一下。这是我们在递归的第 4 层之后所处的位置：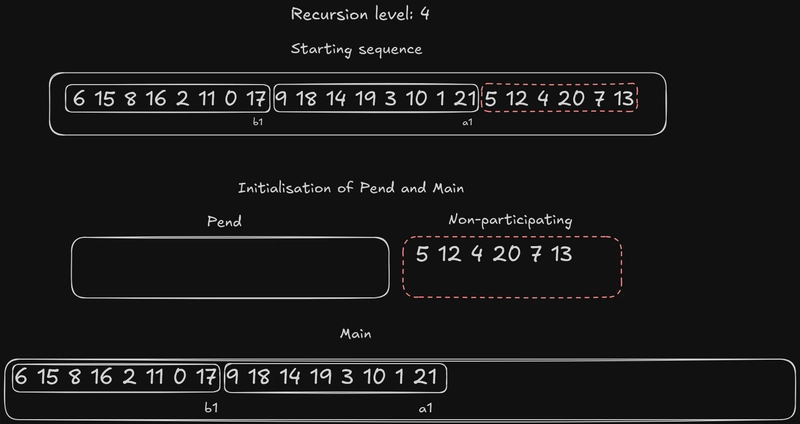

在这个递归层面上，没什么好说的：pend 为空，因为只有两个元素直接指向the main，b1它们a1都属于the main。原因在于我们已经知道b1小于a1，并且根据算法的逻辑（以及你将在后续可视化中看到的内容），the main是有序的，所以a1小于任何其他a，因此不需要额外的比较。所谓“有序”，是指每个元素中最大的数字：在本例中， 和b1中最大的数字分别a1是17和21。这是该算法优化的一个方面，旨在最大限度地减少比较次数。

红色虚线边框内的数字5 12 4 20 7 13是无法组成任何元素的数字。就像步骤 1 中一样，它们仍然是序列的一部分，只是不参与插入操作。

需要理解的一点是，在这一步骤中，当我们初始化the pend并the main更改标签时，由于元素的交换和插入操作，它们的位置会相对于第一步的位置发生变化。在这一步骤中，您可以将标签理解为元素的位置：例如，在这一层级，元素由 8 个数字组成，因此标签b1始终包含位置 0-7 的数字，而标签始终a1包含位置 8-15 的数字b2，依此类推。

在这个递归层级，步骤 3 没什么好说的，因为里面没有任何元素the pend。不pend，不需要插入任何元素。继续下一步。等到有元素需要插入的时候，我会讨论插入逻辑。

第四关已经完成：这里没什么可做的了。

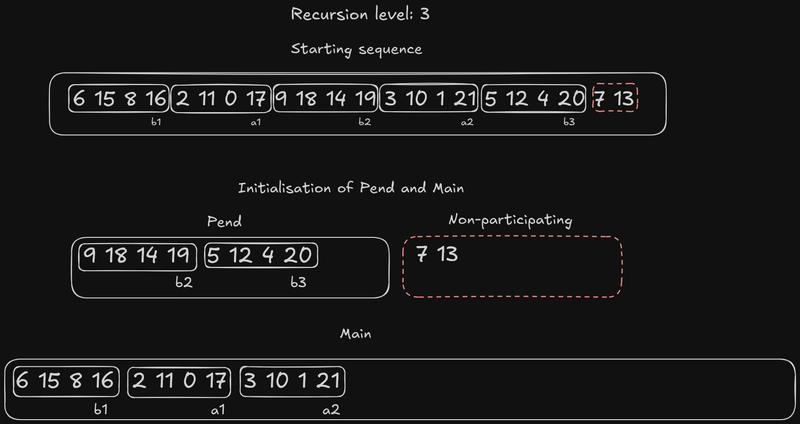
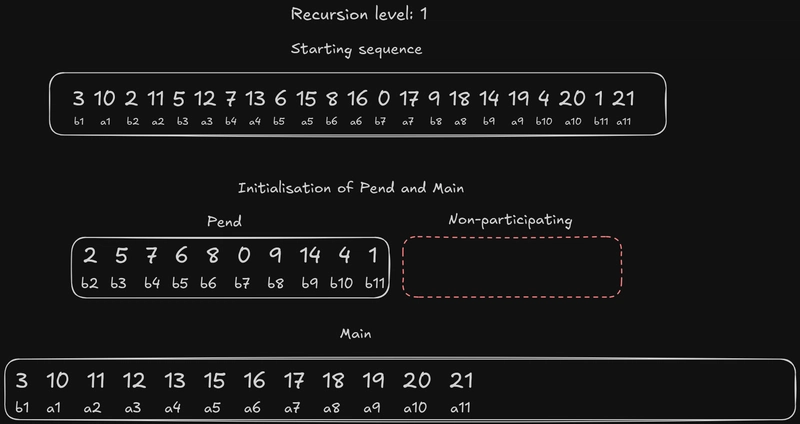
在这一层级，我们的元素由 4 个数字组成。一开始，我们将元素分成bs 和as'。我们初始化the pend，the main正如我之前所说：the main是sb1的其余部分a，the pend是 s' 的其余部分b。注意bs 和as' 的值发生了变化。还记得我之前讲过的重新标记吗？我们在每个递归层级的第二步更改标签。但是请注意，实际的数字对并没有被打破。

这次我们有两个元素the pend：b2+ 一个特殊元素，它没有参与第一步，但在这里是完全参与者。这里需要插入一些东西，以便我们讨论第三步是如何运作的。

步骤 3 可能比较令人困惑。这里就用到了我们归并插入算法中的二分插入。二分插入是什么意思呢？它指的是我们对已排序的序列使用二分查找算法main，来找到元素插入的位置。插入操作本身与二分插入排序pend非常相似，但有一个区别：插入顺序是由称为雅各布斯塔尔数的数学序列决定的。the pend

在继续之前，让我们花点时间了解一下这里发生了什么。为什么要用雅各布斯塔尔数？为什么要用到它们，它们在排序中有什么作用？

为什么是雅各布斯塔尔数？

Ford-Johnson 算法利用了二分查找算法的一个重要优化，进一步减少了元素之间的比较次数。二分查找的最大比较次数对于 n和 n+1 都相同。这意味着 4 和 72^k的2^(k+1)-1最大比较次数相同。8 和 15、16 和 31 也一样……等等。该算法在插入阶段会尽可能地利用二分查找的这一特性。我说的“尽可能地”是什么意思呢？嗯，正如你所记得的，我们在展开第 4 层和第 3 层递归时并没有使用任何雅各布斯塔尔数。等等，但是这些该死的数字和这个优化有什么关系呢？结果表明，如果按照雅各布斯塔尔数规定的特定顺序插入元素，并且我们尊重边界元素，则插入的表面积几乎适用于所有元素，而不是像通常那样只适用于第一个元素，而对于后续元素则完全未知，因为我们会像常规二进制插入一样简单地插入数字（就像我们在递归级别 3 的插入过程中所做的那样）。2^22^3-1the pendthe main2^(k+1)-12^k

雅各布斯塔尔数决定插入顺序的方式如下：我们从雅各布斯塔尔数 3 开始。我们从元素 开始插入元素b3。我们从该元素开始按相反的顺序插入元素，直到遇到b前一个雅各布斯塔尔数对应的元素。换句话说，插入的元素数量为current_jacobsthal - previous_jacobsthal。
对于雅各布斯塔尔数 3，我们插入 2 个元素 (3 - 1)，即b3, b2。
对于雅各布斯塔尔数 5，我们插入 2 个元素 (5 - 3)，即b5, b4。
对于雅各布斯塔尔数 11，我们插入 6 个元素 (11 - 5)，即b11, b10, b9, b8, b7, b6。
希望您理解了。并且现在您应该明白，我们不能总是用这种方式插入数字。如果没有足够的元素可以插入，例如，雅各布斯塔尔数是 11（我们应该插入 6 个元素），但我们只有 3 个元素the pend，那么我们需要以某种方式处理这种情况，最简单的方法是按the pend顺序插入元素，就像我们在递归级别 3 中所做的那样。

好的，但是现在我们再来看一下，这种顺序究竟是如何优化二进制插入操作的比较次数的呢？让我们看看如果按照这个特定顺序插入待插入元素会发生什么！是时候再举个例子了！耶！ 在这些例子中，元素是按标签排序的，但实际的顺序和数字可能更混乱，所以为了清晰起见，例子中是这样排列的。 正如你所看到的，正是雅各布斯塔尔数决定的顺序使得我们可以在算法中使用这种优化：我们可以只对元素进行二分查找，就能将大量待插入元素插入主数组。这是因为根据算法的工作原理，我们知道的边界是。所以当我们插入元素时，例如，与其在搜索范围内查找，不如在搜索范围内查找，因为我们知道没有必要将元素包含在搜索范围内，而且后面的任何元素都肯定更大。插入一个元素后，当需要插入下一个元素时，边界值会减小 1（从变为），但元素数量会增加 1（因为我们插入了），所以该范围内的元素数量保持不变。 注意：然而，正如我们稍后将看到的，雅各布斯塔尔数插入保证了最坏情况下的稳定性。在最佳情况下，如果插入的元素大于搜索范围内的任何其他数字，则搜索范围甚至可能更小。那么，对于下一个数字，搜索范围实际上会更小。您将在接下来的执行过程中看到这一点。


2^(k+1)-1bxaxb5{b1, a1, b2, a2, b3, a3, a4, a5, a6, a7, ...}{b1, a1, b2, a2, b3, a3, a4}a5b5b4a5a4b5
2^(k+1)-1

既然我们已经了解了雅各布斯塔尔数在这里的用途，我想指出，计算第n个雅各布斯塔尔数也存在一种最优方法。四舍五入的结果(2^(n+1) + (-1)^n) / 3会在我们的用例中产生一个偏移量的雅各布斯塔尔数（通常从0开始）。

回到我们离开的地方

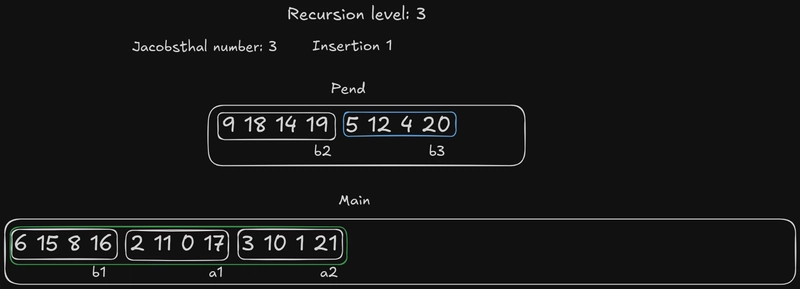
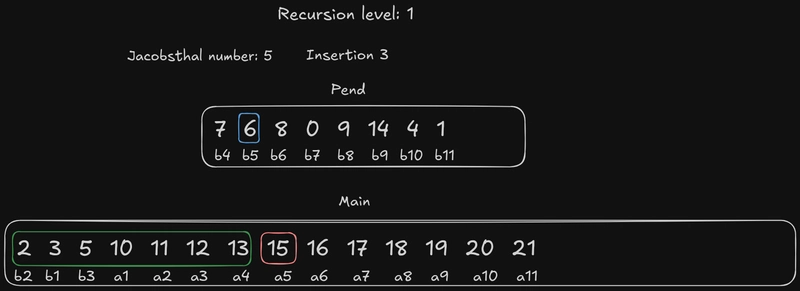
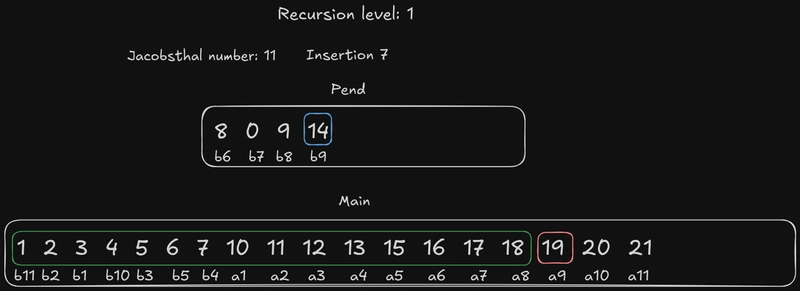
我将用蓝色边框标记当前要插入的元素the pend。绿色边框表示我们将尝试插入该元素的元素范围，a红色边框表示“边界”元素，即对应的元素。“边界”标记了搜索区域的结束。

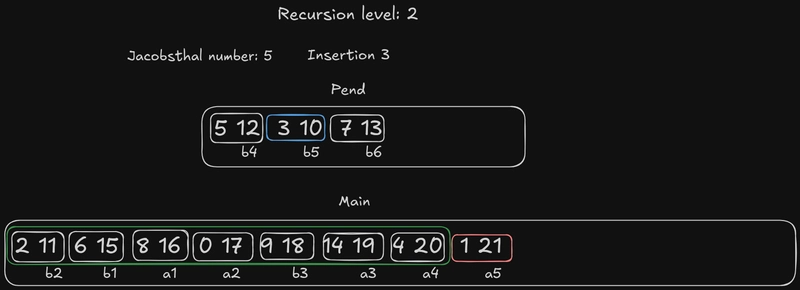
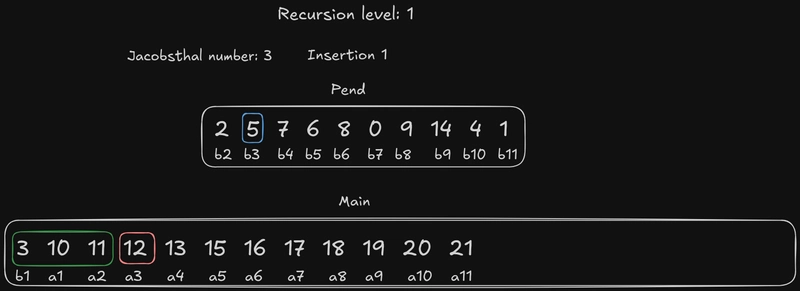
当前的雅各布斯塔尔数是 3，这意味着我们从 开始b3。the pend的边界元素b3是a3，我们应该尝试将其插入。由于 是一个奇数，所以{b1, a1, a2}没有元素，因此我们将其与整个 进行比较。a3b3main

换句话说，我们应该将20元素中的最大数字与{16, 17, 21}搜索区域中元素中的最大数字进行比较，然后将整个元素插入到相应的位置。

由于20大于16或17，我们将整个元素b2（5 12 4 20）插入到a1（2 11 0 17）和a2（3 10 1 21）之间。

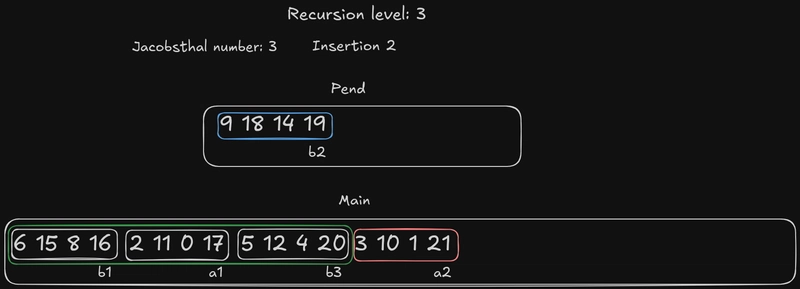
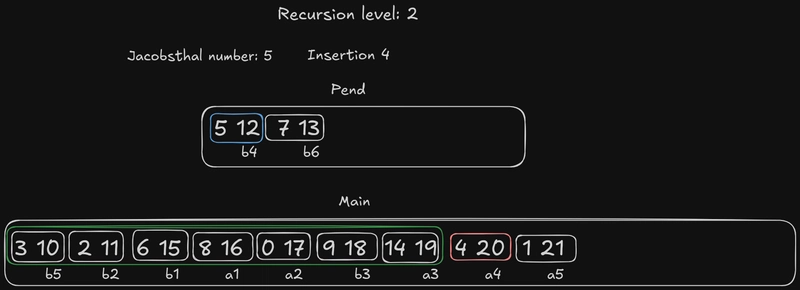
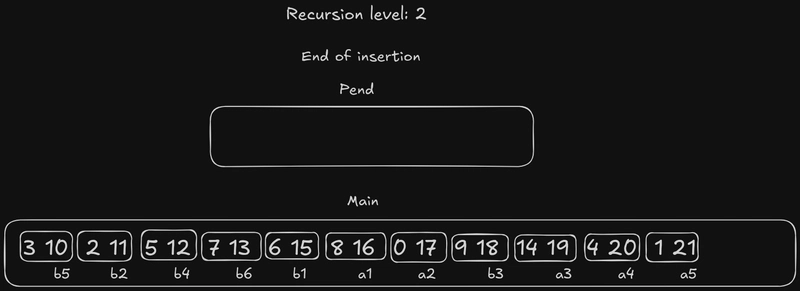
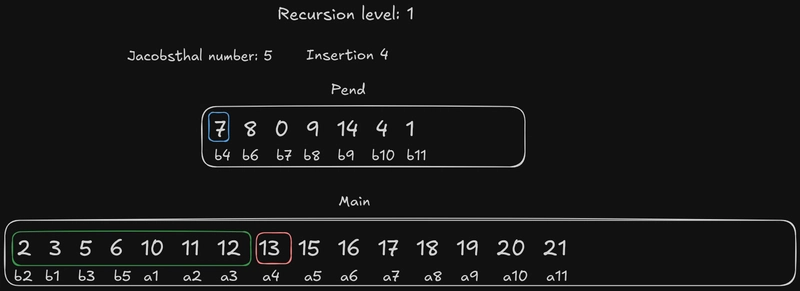
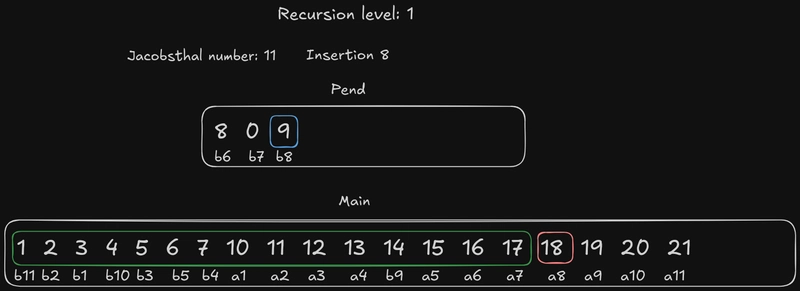
雅各布斯塔尔数仍然是 3，下一个要插入的元素是b2。它的边界元素是a2：我们已经知道它比这个元素小，所以我们尝试把它插入到 中{b1, a1, b3}。

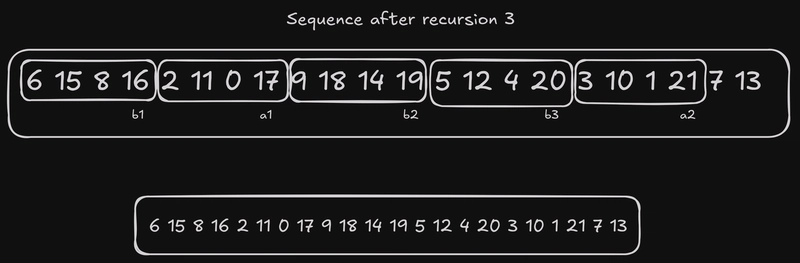
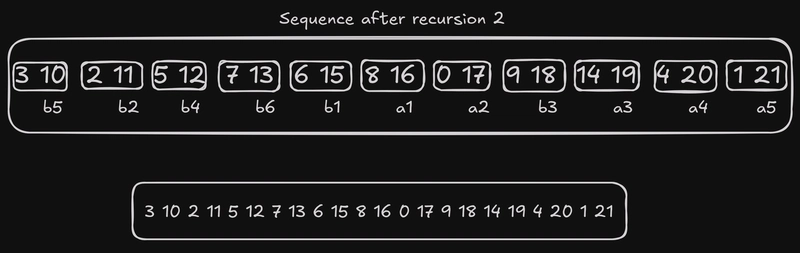
所以，目前我们的序列是这样的：6 15 8 16 2 11 0 17 9 18 14 19 5 12 4 20 3 10 1 21 7 13。当我们向下递归一层时，初始化the main和the pend插入操作都将从这个序列开始。

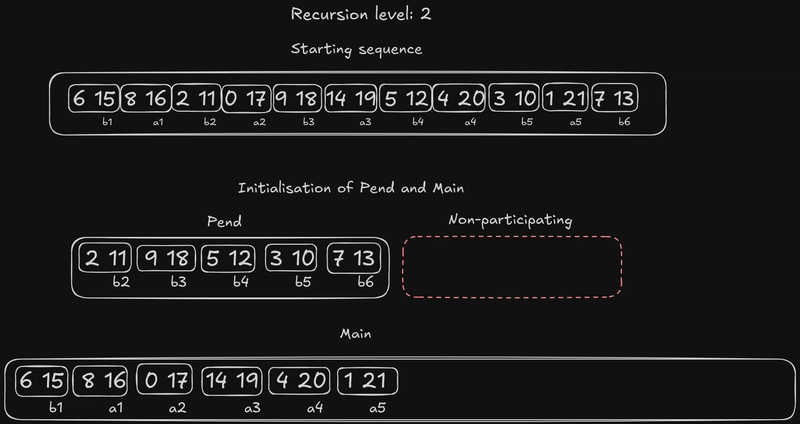
我们将得到的序列再次分解为元素，并初始化main和pend。自递归层数为 3 以来，序列及其标签都发生了变化：但原始的元素对（例如）仍然保持不变。因此，元素（现在是 ）小于元素（现在是）((2 11) (0 17))的保证仍然有效。(2, 11)b2(0, 17)a2

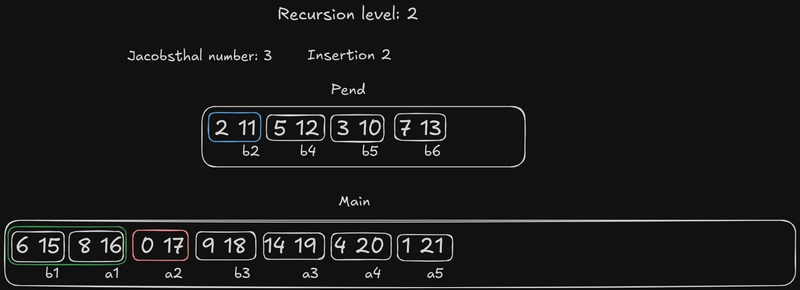
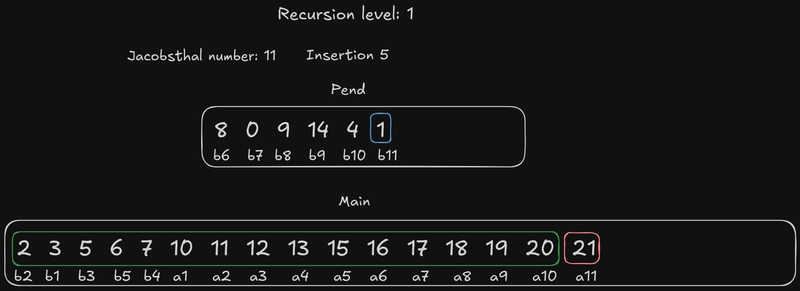
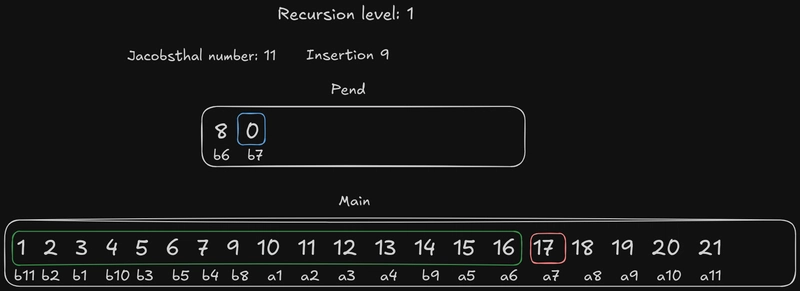
所以，我们将元素插入b3到数组中the main，但正如你所看到的，这缩小了元素的搜索范围b2，因为这个元素比原元素大a2，所以搜索范围缩小了。还记得“为什么是雅各布斯塔尔数？”部分提到的吗？这就是一个例子。这种情况有时会发生，这是该算法中另一个需要注意的棘手之处。

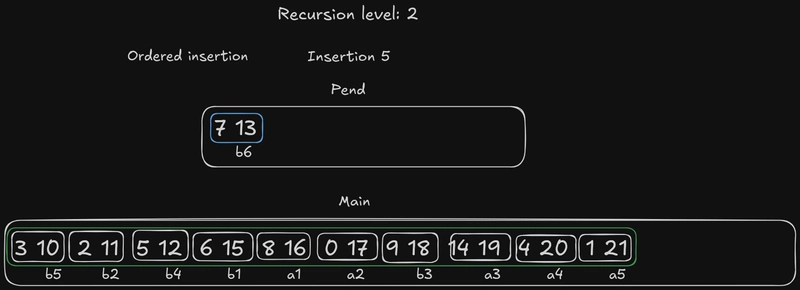
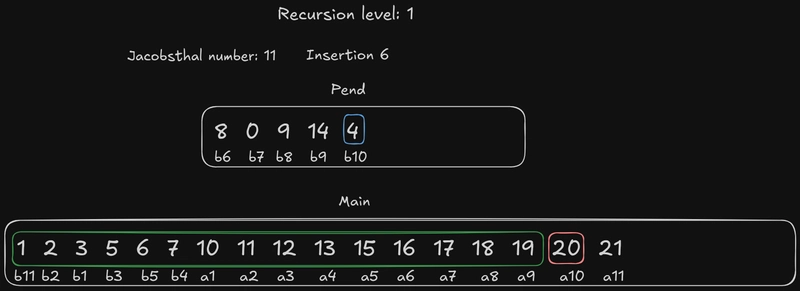
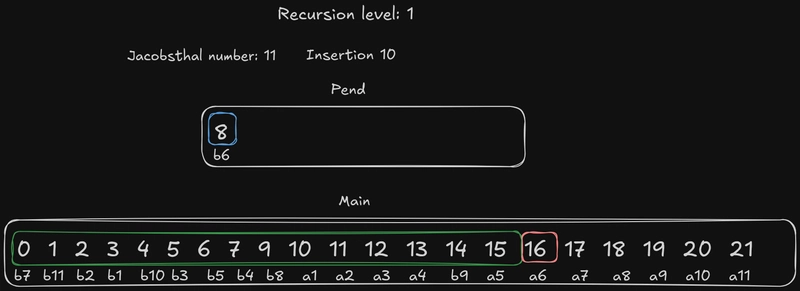
糟糕！雅各布斯塔尔数用完了。数组里只剩下一个元素了the pend！怎么办？我们几乎可以像二分查找那样操作：插入the pend元素，但顺序相反，也就是说我们从末尾开始。这样做是为了保持搜索区域不变。当然，仍然要考虑边界元素：例如，如果我们b3这样插入，搜索区域仍然不包含a3第n个元素。在这种情况下，它是一个奇数，所以没有对应的边界元素。

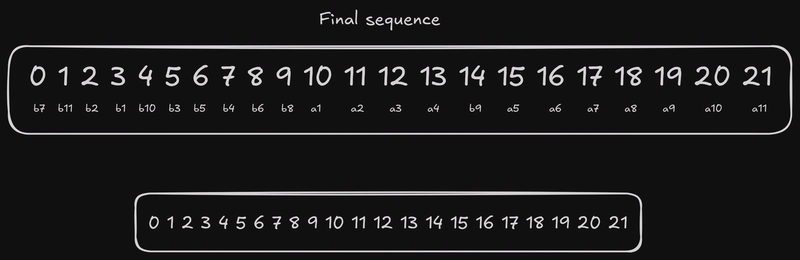
好了，现在，我想我们已经完全具备理解算法其余部分的能力了，所以让我们不再多说，直接开始执行它的步骤吧！

至此，递归的第二层被解决。经过这一层之后的序列如下所示：

这样，我们的序列就排序完成了。这个算法理解起来并不容易，实现起来也不容易，但交换和插入操作都遵循特定的模式，这些模式的特点可以通过反复在纸上或你常用的文本编辑器中演算出来。我鼓励你这样做，因为实践是真正巩固理论的唯一途径。

测试算法实现

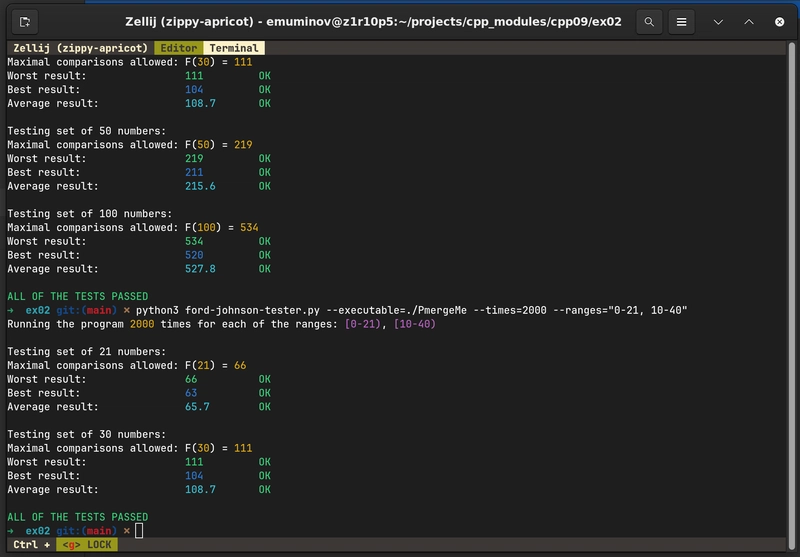
k这是一个最小比较排序算法，因此对于输入的数字，你的算法最多只需要进行 66 次比较n。例如，对于 21 个数字，最大比较次数为 66，所以如果你用 21 个随机数运行此算法 1000 次，比较次数永远不会超过 66 次。

k给定 ，可以用数学方法计算n。该公式由 Knuth 在他的书中描述，而该公式又由 A. Hadian 于 1969 年发现。

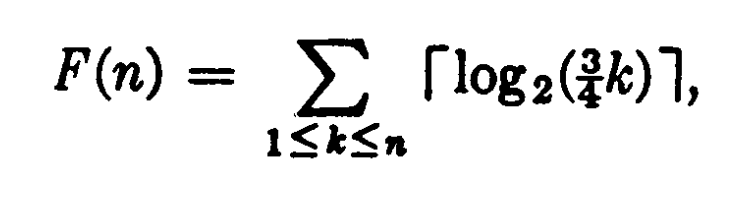
对于不擅长数学的人来说：这个公式其实用代码实现起来非常简单。懂数学的人只是喜欢用简洁而神秘的符号。
用 C++F(n)可以这样写：

#include <cmath>

int F(int n)
{
    int sum = 0;
    for (int k = 1; k <= n; ++k) {
        double value = (3.0 / 4.0) * k;
        sum += static_cast<int>(ceil(log2(value)));
    }
    return sum;
}

下一步是在代码中实现一个比较函数，其目的很简单，就是在每次调用时递增某个全局/静态变量。每当需要比较数字时，包括将其传递给 `match`std::upper_bound或类似函数（如果您打算使用的话），您都需要用到它。

n对于给定的参数，使用不同的参数多次运行函数n，并将比较次数最多和最少的比较结果与预期的最大比较次数进行比较。如果结果超过预期，则说明你的实现还不正确。

我还编写了一个单文件测试脚本来对算法进行基准测试。该脚本要求你的可执行文件在程序结束时打印出排序后的序列和比较次数。

以下是我在代码中计算比较次数的一个示例：

//////////// ADD COMPARISON COUNTER ////////////
// PmergeMe.hpp
class PmergeMe
{
  public:
// ...
    static int nbr_of_comps;
// ...

template <typename T> bool _comp(T lv, T rv) {
    PmergeMe::nbr_of_comps++;
    return *lv < *rv;
}

// PmergeMe.cpp don't forget to initialise it!
int PmergeMe::nbr_of_comps = 0;

//////////// USE _comp FOR COMPARISONS ////////////
// PmergeMe.hpp
// ... at the step 1
        if (_comp(next_pair, this_pair))
        {
            _swap_pair(this_pair, pair_level);
        }
// ...

// ... at the step 3 whenever I search a place for a number to insert into
            typename std::vector<Iterator>::iterator idx =
                std::upper_bound(main.begin(), bound_it, *pend_it, _comp<Iterator>);
// ...

代码

我在完成第 42 学期第 9 模块的最后一个 C++ 练习时实现了这个算法；你可以在这里找到我的实现，即 cpp09/ex02。实现这个算法的方法有很多，我的方法是针对向量进行了优化，并且能够充分利用随机访问。

最后一点

感谢epolitze校对文章初稿，sponthus校对第二稿，以及eandre协助我更新图表。这是文章的第二版，我简化了一些解释（希望这样更清晰易懂），并修正了bwerner
指出的一个错误。

算法最初的描述是，当雅各布斯塔尔数用完时，会the pend以相反的顺序插入元素。在之前的文章版本中，我曾说过根据我的基准测试，这不会造成任何影响；但我错了！在编写了一个能够严格测试数字范围的测试程序并进行多次测试后，我发现顺时针和逆时针插入实际上会产生影响。由于当时没有任何相关的文章或视频，因此在开发这个算法时，我不得不探索未知领域。