从非计算机科学角度看大O符号
大家好!
欢迎来到数据结构与算法系列的第二篇文章!上次我们回顾了JavaScript 数组和字符串中的交叉操作。这次我们将探讨大 O 表示法,深入研究时间复杂度和空间复杂度。
我和梅根都从编程训练营毕业,学习了 Ruby on Rails、JavaScript、React 等技术后,我们花了很多时间通过各种在线资源学习大 O 表示法。如果您正在寻找大 O 表示法的“通俗易懂”的解释,希望这里能帮到您!
介绍
在计算机科学中,大O符号用于描述算法运行时间和空间需求随输入规模增长而变化的情况。大学计算机科学专业的学生需要学习不同类型的大O符号(例如大O、大θ、大Ω)。但在软件工程技术面试中,我们只关注最佳情况和最坏情况,而大O符号能够最精确地描述算法的运行时间和空间需求。
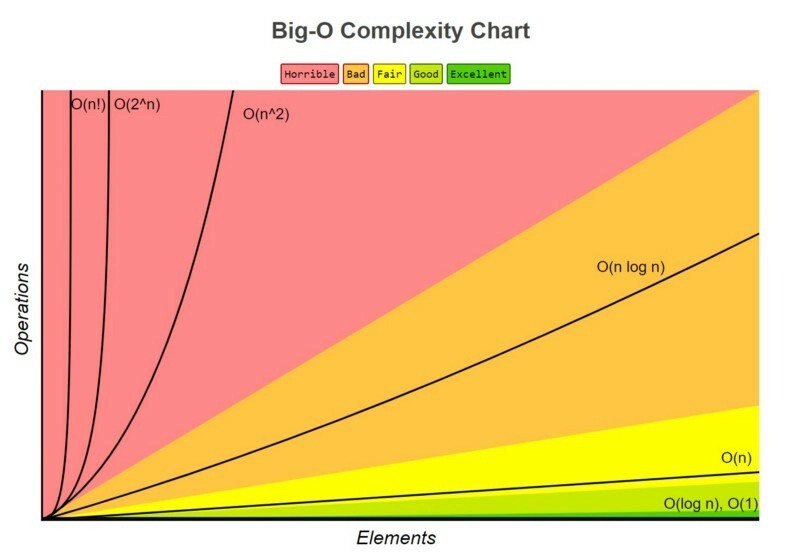
该图清晰地展示了运行时间和空间复杂度如何随大O表示法的输入而变化。O(1)和O(log n)具有最佳的运行时间和空间复杂度O(n!),而 和具有最差的运行时间和空间复杂度。O(n2)O(2n)
在本文中,我们将逐一讲解这些符号,并在每个部分末尾提供示例和 LeetCode 问题。
蛮力法和优化解法分别是什么意思?
在开始之前,我们想解释一下什么是蛮力解法和优化解法,因为您可能会在文章后面看到这些关键词。
理解暴力解法最简单的方法就是想到什么就用什么。另一方面,对于优化解法,在找到暴力解法之后,你会考虑如何优化代码,尽可能地降低时间和空间复杂度。
例如,你的暴力破解方案的时间复杂度为 O(n),而优化后的方案可以将时间复杂度降低到 O(n) 。 理解这个概念很重要,因为你需要和面试官讨论如何将暴力破解方案优化为更优的方案。O(n2)O(n)
复杂度比较
| 姓名 | 大O符号 |
|---|---|
| 恒定时间 | O(1) |
| 对数时间 | O(log n) |
| 线性时间 | 在) |
| 线性时间 | O(n log n) |
| 二次时间 | O(n 2 ) |
| 指数时间 | O( 2n ) |
| 阶乘时间 | 在!) |
恒定时间:O(1)
通常被称为“恒定时间”函数,O(1)复杂度最低。我喜欢这样理解:无论输入数据量大小,函数内部执行的步骤数始终相同。
例子:
function sayHelloToFirstFriend(friends) {
return `Hello ${friend[0]}`
}
sayHelloToFirstFriend([“spongebob”, “patrick”, “sandy”, “squidward”, “gary”])
// “Hello spongebob”
对数时间:O(log n)
不要害怕数学!当你看到对数时,它其实是在问你:“为了得到这个答案,这个底数必须上升到多少次方?”换句话说,当变量是指数时,我们用对数来求解变量。
在计算机科学领域,这可以转化为:“我们需要将 n 除以多少次才能得到 1?” 因此,解决方案O(log n)本质上是将问题一分为二,确定需要继续处理哪一半,再将该部分除以二,如此反复,直到找到所需结果或排除该集合。因此,虽然这些解决方案的时间复杂度会超过常数,但与其他时间复杂度相比,其增长速度仍然很慢。
| 典型用例 |
|---|
| 二分查找 |
| 某些基于线性函数的分治算法 |
| 计算斐波那契数列 |
注意:请注意,在所有这些用例中,输入都是已排序的,并且正在搜索某些内容!
线性时间:O(n)
最常见的可能是O(n)线性时间。这是因为随着输入规模的增长,执行操作所需的时间也会增长。换句话说,如果一个数组有 10 个元素,那么 for 循环将执行 10 次;而如果数组有 10,000 个元素,同样的 for 循环也将执行 10,000 次。
例1:
const binarySearch = (list, target) => {
let start = 0
let end = list.length - 1
while (start <= end) {
const middle = Math.floor((start + end) / 2)
const guess = list[middle]
if (guess === target) {
return middle
}
if (guess > item) {
// search the right side of the list
end = middle - 1
} else {
// search the left side of the list
start = middle + 1
}
}
return null // if target is not found
}
例2:
function sayHelloToFriends(friends) {
for (let i = 0; i < friends.length; i++) {
console.log(`Hello ${friends[i]}`)
}
}
sayHelloToFriends([“spongebob”, “patrick”, “sandy”, “squidward”, “gary”])
// “Hello spongebob”
// “Hello patrick”
// “Hello sandy”
// “Hello squidward”
// “Hello gary”
线性对数时间:O(n log n)
基于典型的排序算法O(log n),额外的“n”代表排序所需的额外时间成本。因此,许多排序算法的复杂度为O(n^2) O(n log n)。另一方面,虽然O(n^2)算法的时间复杂度确实比O(n^2)算法高O(log n),但需要注意的是,对数增长速度非常慢。因此,O(n^2)算法的时间复杂度与线性时间复杂度类似。为了更详细地解释O(n^2)算法的n复杂度关系,我们来看归并排序。
与排序类似O(log n),归并排序首先将数组分成两半。然后对这两半进行排序,最后将排序后的两半合并成一个整体。但是,为了对这两半进行排序,需要重复相同的步骤:分割、排序、合并,直到所有数据都排序完毕。
例子:
function merge(left, right) {
let arr = []
// Break out of loop if any one of the array gets empty
while (left.length && right.length) {
// Pick the smaller among the smallest element of left and right sub arrays
if (left[0] < right[0]) {
arr.push(left.shift())
} else {
arr.push(right.shift())
}
}
// Concatenating the leftover elements
// (in case we didn't go through the entire left or right array)
return [ ...arr, ...left, ...right ]
}
function mergeSort(array) {
const half = array.length / 2
// Base case or terminating case
if(array.length < 2){
return array
}
const left = array.splice(0, half)
return merge(mergeSort(left),mergeSort(array))
}
| 典型用例 |
|---|
| 归并排序 |
| 堆排序 |
| 快速排序 |
| 某些基于优化 O(n²) 算法的分治算法 |
二次时间:O( n² )
时间复杂度为二次方的函数,其增长率为 n² 。这意味着什么呢?如果输入规模为 2,则该函数需要执行 4 次运算。如果输入规模为 3,则该函数需要执行 9 次运算。如果输入规模为 1000,则该函数需要执行 100 万次运算。
换句话说,该函数的运行速度会非常慢,尤其是在输入规模非常大的情况下。O(n2)
大多数情况下,当我们需要至少两次迭代对象时,我们会描述一个时间复杂度为二次方的算法,例如嵌套的 for 循环。
查找重复项和冒泡排序是你会遇到的两个二次方算法的例子。冒泡排序(以及插入排序和选择排序)就像归并排序和快速排序的简单版本。它速度很慢,但通常是你学习排序算法时最先接触的概念。它为学习其他更复杂的排序算法奠定了良好的基础。
冒泡排序的原理是,如果相邻元素顺序错误,就反复交换它们。假设我们要对一个无序的数字数组进行排序,从小到大。冒泡排序会逐个交换数字,检查它们的顺序是否正确。
冒泡排序示例:
function bubbleSort(arr, n) {
for (let i = 0; i < n - 1; i++) {
for (let j = 0; j < n - i - 1; j++) {
if (arr[j] > arr[j + 1]) {
swap (arr, j, j+1);
}
}
}
}
// swap helper method
function swap (arr, first, second) {
let temp = arr[first];
arr[first] = arr[second];
arr[second] = temp;
}
与归并排序(会将数组切成两半)相比,冒泡排序会逐个遍历数组中的每个元素,直到所有元素都排序到正确的位置(即使已经排序完毕,它还会再遍历一次)。
| 典型用例 |
|---|
| 冒泡排序 |
| 插入排序 |
| 选择排序 |
| 查找重复项(暴力破解) |
| 找出数组中所有可能的有序对 |
指数时间:O( 2n )
以2 为底的指数运算时间意味着,随着输入规模的增大,计算量将翻倍。2² => 4;2³
= > 8;2⁴
= > 16 ;……;2¹⁰ = > 1,267,650,600,228,229,401,496,703,205,376
正如你所看到的,每当这个数n加 1,结果就会翻倍。本质上,这个数一开始很小,但最终会变得非常大。
大多数情况下,请避免使用指数时间,因为运行速度会越来越慢。虽然它并非最糟糕的情况,但显然也并非最佳选择。
斐波那契数列示例
function fib(n) {
if (n <= 1) {
return n
}
return fib(n - 1) + fib (n - 2)
}
| 典型用例 |
|---|
| 幂集:求集合的所有子集 |
| 斐波那契数列 |
阶乘时间:O(n!)
如果你理解了阶乘的原理,那么它就是这样的:
5! = 5 × 4 × 3 × 2 × 1,换句话说,
n! = n × (n - 1) × (n - 2) × (n - 3)... × 1
随着输入规模的增大,运行时间也会越来越长!我个人还没有遇到过阶乘问题,因此我会在下面附上一个例子,并附上链接供参考。
| 典型用例 |
|---|
| 排列 |
结论
我们希望这篇文章能帮助你更好地理解大O表示法!这个概念非常重要,因为在面试中,你经常需要分析解决方案的大O表示法。此外,了解大O表示法还能帮助你在构思方案时判断哪个方案的运行时间更优或更差。如果你仍然感到困惑,我们已在下方提供了更多参考资料!
资源
- 复杂度分别为 O(1)、O(n log n) 和 O(log n) 的算法示例 👀 (Stack Overflow)
- Big-O 速查表
- 什么是大O符号?详解:空间复杂度和时间复杂度(FreeCodeCamp)
- 大O符号(维基百科)
- 程序员应该了解的 8 个时间复杂度(附视频和示例)
- 比较两个和问题的不同解法(斯坦福)

