Logo

菜单

发布于 2026-01-06 1 阅读
0

大O符号：质因数分解和伪多项式时间

大O符号：质因数分解和伪多项式时间

大多数程序员至少对大O符号有所了解。这是一种用于在输入规模增大时，寻找算法运行时间和空间需求上限的技术。

我们以排序列表为例：随着待排序元素数量的增加，不同的算法会有不同的表现。一个非常简单的算法可能会遍历列表，找到最小的元素，并将其移到列表的最前面。然后，它对列表的其余部分重复相同的过程。在这种情况下，我们首先遍历大小为 N 的列表来找到最小的元素，然后是大小为 N-1、N-2 的列表，依此类推。这意味着我们需要执行 N × (N+1) / 2 次比较。因此，这样的算法的时间复杂度为 O(N² )，或者说是多项式的（更准确地说是二次的），相对于所需的比较次数而言。从整体来看，这还算不错。然而，还有一些更优秀的算法可以在 O(N × log N) 的时间内完成排序。

总体而言，问题的复杂性可以分为三大类：

  1. 如果算法的时间复杂度为 O(1)、O(log N)、O(sqrt N)、O(N) 或 O(N × log N)，则通常认为这些算法是相当容易处理的，这是一种比较文雅的说法，意思是它们易于管理。

  2. 复杂度至少为二次多项式的算法，例如 O(N² )、O(N³ )等，随着输入规模的增大，求解成本也会增加。这种复杂度虽然并不理想，但只要指数较小，对于许多实际问题来说通常仍然可以接受。

  3. O(2^ N ) 算法需要指数级的资源。这意味着，即使输入规模只有微小的增加，我们也需要不断翻倍地增加资源。复杂度为指数级甚至更高（例如阶乘）的算法通常被认为是难以处理的。计算需求的跃升非常迅速，因此即使拥有强大的计算能力，也只能解决此类问题的少量实例。

有时人们会说大O表示法衡量的是最坏情况下的性能。但这种说法其实存在一些细微差别。大O表示法确实衡量了相对于输入的性能上限。然而，对于不同类型的输入，算法可能具有不同的大O表示法。通常会考虑最佳情况、最坏情况和平均情况。例如，快速排序的最坏情况已知为O(N² )，但通常情况下是O(N × log N)。

在本文中，我想探讨一个可能比较棘手的问题，即大O表示法是相对于输入长度而言的。这意味着，对于同一个算法，大O表示法实际上可能会因输入表示方式的不同而有所差异！这可能听起来有些令人困惑，所以让我们来看一个具体的例子。

整数因式分解

将整数分解为素数是计算机科学中的一个经典问题。一些广泛使用的加密算法，例如 RSA，正是利用了随着数字增大，分解整数变得越来越困难这一特性。传统的整数分解算法在最坏情况下需要指数级的时间复杂度。

因式分解并非NP完全问题。如果拥有数千量子比特的量子计算机成为现实，Shor算法就可以在多项式时间内分解整数。然而，人们普遍认为，即使是量子计算机也无法解决NP完全问题。

让我们来研究一下最直观、最直接的分解质因数的算法。假设我们有一个整数，比如 124。我们如何把它分解成质因数呢？我们可以先检查这个数是否能被 2 整除：

124 / 2 = 62

结果为偶数，所以我们再除以 2：

62 / 2 = 31

从这里我们可以尝试用 3、4、5 等等一直除到 30，但所有这些除数都会有余数。这意味着 31 也是质数。它只能被自身或 1 整除。因此，124 的质因数是 2 × 2 × 31。

仅检查平方根以内的因子

我们可以对这个算法进行一个重要的优化：与其检查所有小于等于 N 的因子（即 N 本身），我们只需检查小于或等于 N 的平方根的数即可。假设 √N = S。根据定义，S × S = N。假设我们有一个大于 S 但小于 N 的整数 T，并且 T 是 N 的一个因子。这意味着 N / T = U，其中 U 也是 N 的一个因子。由于 T 大于 S，U 必定小于 S（否则 T × U 将大于 N）。由于 U 小于 S，我们会在遇到 S 之前就尝试将其作为因子。N / U 的商是 T。因此，我们会在遇到 S 之前就遇到 T。

要找出 N 的所有质因数，我们只需要尝试从 2 到 N 的平方根（包含 2 和 N）的所有可能的因数即可。以下是该算法在 Python 中的简单实现：

def prime_factors(n):
    results = []

    factor = 2
    while factor * factor <= n:
        (n, intermediate_results) = check_factor(n, factor)
        results += intermediate_results
        factor += 1

    if (n > 1):
        results += [n]

    return results

def check_factor(n, factor):
    results = []

    (q, r) = divmod(n, factor)
    while r == 0:
        results.append(factor)
        n = q
        (q, r) = divmod(n, factor)

    return n, results
Enter fullscreen mode Exit fullscreen mode

我们可以通过跳过大于 2 的偶数来进一步将该算法的运行时间缩短一半，因为任何偶数因子都可以通过检查是否能除以 2 来提取。虽然这在实践中可能意义重大，但从大 O 表示法的角度来看，它并不会从根本上改变算法的复杂度。大 O 表示法通常是一种粗粒度的工具，它寻找的是总体增长模式，而常数因子和低阶项往往会被忽略。

最坏情况

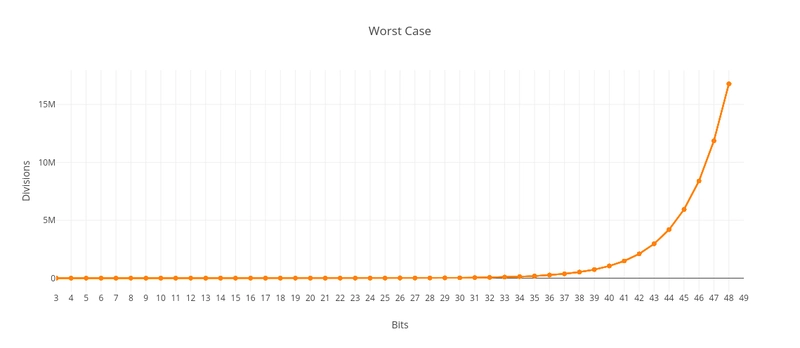
当我们分解一个数 N 时，随着 N 的增大，我们需要执行多少次除法运算？算法最坏的情况是 N 为质数：算法需要尝试（但不会成功）从 2 到 N 的平方根的所有数字。因此，算法在最坏情况下的时间复杂度为 O(√N)。假设我们尝试分解质数 1000003。我们需要检查从 2 到 1000 的每一个数字，因此我们将执行 (√N) - 1 次除法运算。

输入长度与幅度

表面上看，这个算法似乎是亚线性的。然而，有一个容易被忽略的关键问题。编码 N 所需的比特数是 log₂N 。这意味着，即使当我们把除法次数与 N 进行比较时，它是亚线性的，但实际上，除法次数相对于输入长度（以比特为单位）是指数级的。如果我们的算法是 O(N) 的，那么它应该是 O(2b )，其中 b 是 N 的比特数。然而，这里它是 O(√N)。由于 √N 需要的比特数是 N 的一半，所以我们的算法实际上是 O(2b /2 )。

下图显示了最坏情况下除法次数与 N 的位数之间的关系：

最坏情况

我们可以用一元表示法来编码数字，而不是使用十进制或二进制表示法，其中 1 = 1，2 = 11，3 = 111，以此类推。在这种情况下，我们的算法的时间复杂度确实是 O(√N)。然而，我们需要使用比实际需要多得多的内存，而且是指数级增长。在二进制中，1000003 只需要 20 位（11110100001001000011）。而在一元表示法中，它却需要 1000003 位！在十进制中，1000003 需要 7 位，甚至比二进制的 20 位还要少。然而，两者都与数字的对数成正比，因此这种差异对于大 O 表示法来说通常并不重要。例如，要将以 2 为底的对数转换为以 10 为底的对数，我们使用公式 log 10 N = log 2 N / log 2 10 ≈ 1/3.32 × log 2 N。它们彼此成正比。

随着 N 的位数增加，我们需要指数级增加的除法次数才能得到一个数的质因数。当然，随着位数的增加，N 本身的数值也会呈指数级增长。这就是为什么这类算法有时被称为伪多项式算法。为了观察所需除法次数呈指数级增长的影响，我们必须不断增加位数，从而处理极其庞大的数字。我认为，这里需要注意的关键是，N 本身才是实际的输入，而不是一个包含 N 个元素的列表。

伪多项式时间算法只有在遇到包含“指数级大”数字的实例时才会表现出“指数行为”，而这种情况在我们感兴趣的应用中可能很少见。如果真是如此，这类算法或许能像多项式时间算法一样满足我们的需求。—— 《计算机与难解性》 ，迈克尔·R·加里和大卫·S·约翰逊著

典型

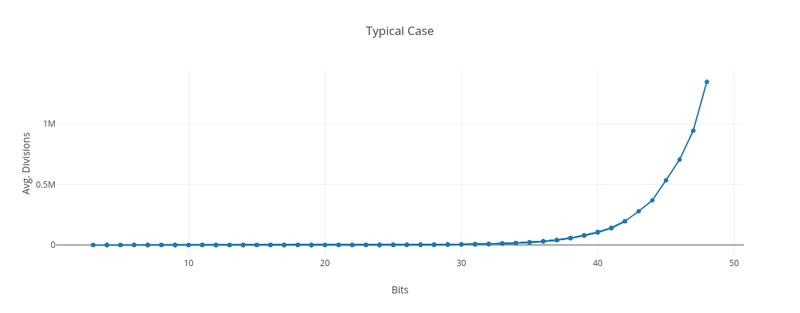
我不知道如何用解析方法确定典型或平均情况下的复杂度函数（大O符号），但我尝试做了一些模拟来大致了解情况。我们可以看到，曲线仍然呈指数形式。

典型

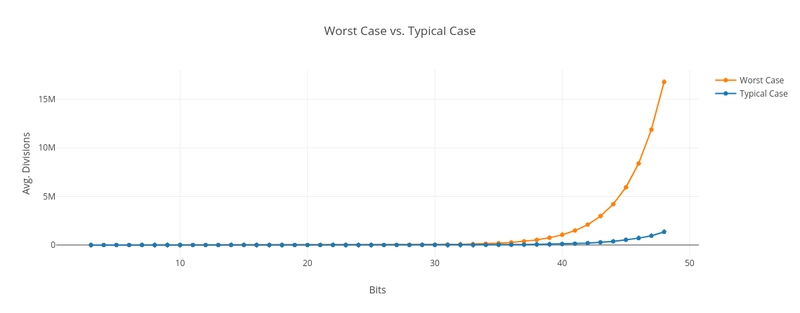
显然，这比最坏情况要好得多。下图展示了最坏情况与典型情况粗略估计值的对比。我生成了 2<sup> b-1</sup> <= N < 2<sup> b</sup>范围内的随机数，其中位数 b 从 3 到 48。对于每个位数，我分解了 10,000 个随机生成的数字。我们可以看到，随机数的除法次数比素数少得多：

最坏情况与典型情况

我认为原因在于，随着数字位数的增加，我们需要检查的候选因子所占的比例呈下降趋势。它肯定远小于√N。直觉上，这对我来说也说得通，因为我们预期给定范围内的随机数的小质因子会比大质因子多得多。

这些结果实际上非常接近于我们使用预先存在的质因数列表进行试除法时的预期结果。在这种情况下，复杂度不是 O(2b /2 )，而是 O(2b /2 /b × 2/ln 2)。这表明，当我们随机选择数字时，大多数情况下我们实际上只需要检查一个相对较小的质数列表即可。

此外，每次找到一个质因数后，我们都会将需要考虑的因数范围缩小到前一个商的平方根。在很多情况下，这可以迅速减少除法次数。

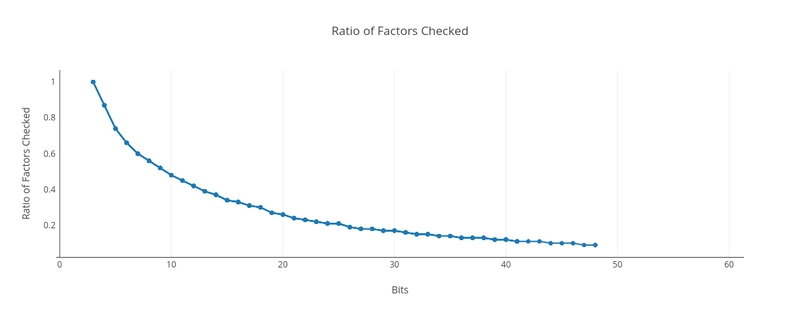
下图显示了实际检查的因子数与√N的比值。对于3位数，例如100（4）、101（5）、110（6）和111（7），只需要检查一个因子2。由于我们始终只检查这一个因子，因此比值为1，即100%。随着数字越来越大，我们需要检查的候选因子比例急剧下降，并且随着位数趋于无穷大，该比例趋近于零：

检查的因素百分比

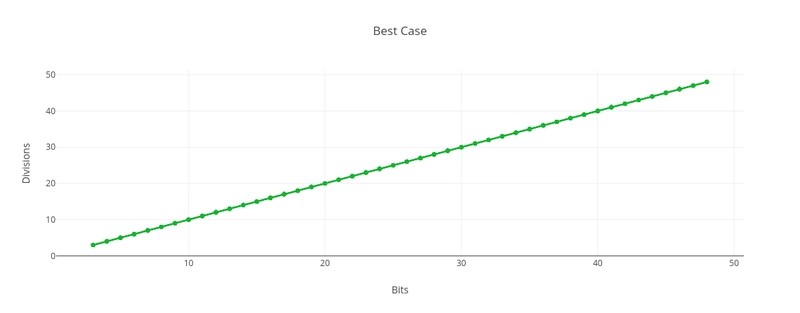
最佳情况

在最佳情况下，输入是 2 的幂，因此只需要不断地除以 2。对于数字 N 而言，这意味着我们只需要进行 log₂N次除法。我们的算法对于 N 的大小而言是 O(log N)，对于 N 的位数 b 而言是 O(b)。虽然最坏情况下的时间复杂度是指数级的，但最佳情况下的时间复杂度是线性的。

最佳情况

除法并非恒定不变

本文以求得一个数的质因数所需的除法次数为框架展开，假设每次除法所需的运算量都是恒定的。对于可以直接用机器指令进行除法运算的数来说，这种假设是合理的。例如，如果计算机有一条 64 位除法指令，那么我们用哪两个 64 位数相除都无关紧要。

然而，对于非常大的数字，这种方法就失效了。如果我们用长除法之类的简单方法来除两个（巨大的）数字，时间复杂度会变成 O(b²)，其中 b 是这两个数字的位数。我相信使用更高级的技术可以改进这一点，但仍然会比 O(b × log b) 更差。不过，由于我们的质因数分解算法是指数级的，这个额外的因子可能太小，不足以显著改变结果。指数项往往会掩盖任何额外的多项式因子。

结论

尽管存在一些更高效的算法来求极大数的质因数，但实际上，在一般情况下，它们的计算复杂度仍然基本呈指数级增长。在没有量子计算机的情况下，目前还没有已知的有效分解数字的方法。RSA 加密算法正是利用了这一原理：RSA 生成两个非常大的质数（每个质数都达到数千比特），然后将它们相乘。它依赖于找出这两个巨大乘积的两个质因数的难度。

人们初次接触大O表示法时，很容易忽略输入编码方式中的一些细微之处。我希望这篇文章能在这方面有所帮助。

背包问题的动态规划算法是伪多项式时间算法的另一个例子。

大O的介绍

如果你之前没有接触过大O符号的概念，这里有两篇dev.to上的热门文章，介绍了大O符号和复杂度的概念：

参考

文章来源：https://dev.to/nestedsoftware/big-o-prime-factors-and-pseudo-polynomial-time-55cp
如何在 JS (vue) 文件中使...
默认函数参数（ES6）