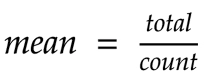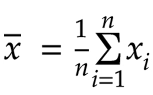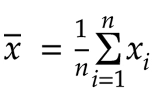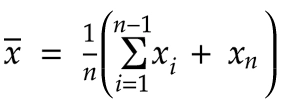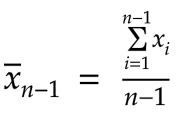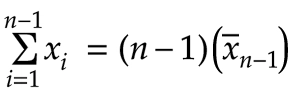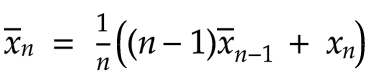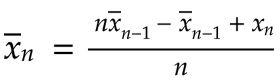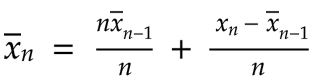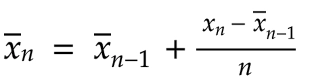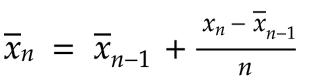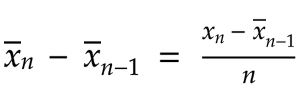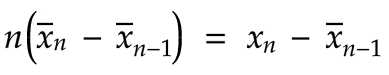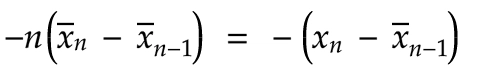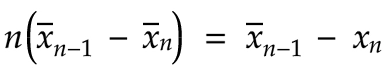计算流数据的移动平均值

最近我需要对一系列输入数据进行一些统计计算（平均值和标准差）。我做了一些研究，这篇文章就是研究成果。我将文章分成几个部分。第一部分介绍如何逐步计算平均值。第二部分将介绍如何逐步计算标准差。第三部分将介绍指数移动平均法，也称为低通滤波器。

人们通常所说的“平均值”，在统计学中更专业的说法是“算术平均值”。在本文中，“平均值”和“均值”这两个术语可以互换使用。

我们通常在学校里学到的计算一组数据平均值的方法是，将所有数值（总数）相加，然后除以数值的数量（计数）：

以下是描述我上面所写内容的数学符号：

下面这个简单的 JavaScript 函数使用了这种简单的方法来计算平均值：

const simpleMean = values => {
    validate(values)

    const sum = values.reduce((a,b)=>a+b, 0)
    const mean = sum/values.length
    return mean
}

const validate = values =>  {
    if (!values || values.length == 0) {
        throw new Error('Mean is undefined')
    }
}

这种逻辑本身没有问题，但在实践中却存在一些局限性：

我们累积的金额可能很大，这在使用浮点类型时可能会导致精度和溢出问题。
我们需要先获得所有数据才能进行计算。

这两个问题都可以用增量式方法解决，即根据每个新值调整平均值。我先用一些数学知识推导出这个公式，然后再展示一个 JavaScript 实现。

数学中常用两个符号来表示平均值。σ小写希腊字母 σ 指的是总体均值，即所有可能值的平均值。例如，某次考试所有成绩的平均值就是一个总体均值。

x̄样本均值（读作 x-bar）是指样本平均值。它是从总体中抽取的样本值的平均值。例如，你可以随机抽取全国一部分人来计算平均身高，但测量全国每个人的身高是不切实际的。当然，在使用样本时，我们希望样本均值尽可能接近其所代表的总体均值。

我决定在本文中使用样本符号，以表明我们计算的平均值可能基于样本。

好的，我们先从之前看到的平均值公式开始：

让我们把总和分成两部分，先把前 n-1 个值加起来，然后再把最后一个值 x _n加起来。

我们知道平均值 = 总数 / 计数：

我们稍微调整一下顺序：

以下是对前 n-1 个值的总和应用上述替换后的结果：

让我们进一步展开讨论：

稍作调整，我们得到：

我们可以约掉n第一个分数中的单引号，得到最终结果：

这一切究竟意味着什么？我们现在有了一个递推关系，它定义了第 n 个值的平均值，如下所示：将前 n-1 个值的平均值加上一个差值。每次添加新值时，我们只需计算这个差值并将其加到前一个平均值上。这样就得到了新的平均值。

以下是这一想法的简单实现：

class MovingAverageCalculator {
    constructor() {
        this.count = 0
        this._mean = 0
    }

    update(newValue) {
        this.count++

        const differential = (newValue - this._mean) / this.count

        const newMean = this._mean + differential

        this._mean = newMean
    }

    get mean() {
        this.validate()
        return this._mean
    }

    validate() {
        if (this.count == 0) {
            throw new Error('Mean is undefined')
        }
    }
}

在上面的代码中，每次我们update用新值调用函数时，计数都会加一，并计算差值。newMean是之前平均值加上这个差值。这就会成为下次调用函数时要使用的平均值update。

以下是对这两种方法的简单比较：

console.log('simple mean = ' + simpleMean([1,2,3]))

const calc = new MovingAverageCalculator()
calc.update(1)
calc.update(2)
calc.update(3)
console.log('moving average mean = ' + calc.mean)

结果符合预期：

C:\dev\>node RunningMean.js
simple mean = 2
moving average mean = 2

当然还有许多其他类型的移动平均线，但如果您只是想要一个累积移动平均线，那么这种逻辑效果很好：它很简单，您可以将其应用于流式数据集，并且它避免了朴素方法可能出现的精度和溢出问题。

在结束之前，我想利用我们上次的结果推导出另一个恒等式。我们现在用不到它，但我们会在下一篇文章中用到它。

我们先从均值的递推关系式开始：

让我们从等式两边减去右边的第一项，这样就能得到微分的值：

现在我们乘以 n：

让我们将等式两边同时乘以-1：

最后，让我们将等式两边同时乘以 -1：

我们暂时先记住这个恒等式，但它在第二部分中会很有用，在第二部分中我们将推导出逐步计算方差和标准差的公式。