如果用 Rust 编写 SQLite 会是什么样子?——第三部分
数据结构是优秀程序的关键。
那么,我们开始吧!
我们先来谈谈二叉搜索树。
什么是B树?以及为什么需要B树?
概括
用 Rust 从零开始编写一个SQLite克隆版本
← 第一部分 — 了解 SQLite 并设置 CLI 应用程序和 REPL
在 GitHub 上查看(非常欢迎提交 pull request)
好了,我们正一步步接近目标。我们的目标是创建一个基于 SQLite 的简单关系型数据库,这意味着它需要嵌入到一个单独的文件中。这次,除了之前文章中提到的研究之外,我还花了很多时间研究所有与 SQLite 相关的内容,例如:文档、代码库和相关讨论。
自本系列最后一章以来,我还花了很多时间去了解关系数据库中使用的数据结构的基本原理,它们在 SQLite 中的使用方式,以及在 SQLRite 项目中采用它们的最佳方法。
数据结构是优秀程序的关键。
我非常提倡围绕数据设计代码,而不是反过来,我认为这正是 Git 能够取得相当成功的原因之一……事实上,我认为优秀程序员和糟糕程序员的区别在于,前者更重视代码本身,还是更重视数据结构。 糟糕的程序员只关注代码,而优秀的程序员则关注数据结构及其相互关系。
如果你还需要更多,这里还有罗布·派克在1989年写的一篇文章:
数据才是关键。如果你选择了正确的数据结构并妥善组织了数据,算法几乎总是显而易见的。 数据结构,而非算法,才是编程的核心。
我认为他们在软件方面确实很有见地,你同意吗?总之,我的理解是,好的数据结构能让代码的设计和维护变得轻松,而世界上最好的代码也无法弥补糟糕的数据结构。我认为这和我第一部分提到的“只要花足够的时间规划,编码就很容易”也相呼应。
因此,在本系列的这一章中,我们将深入探讨数据库设计中使用的主要数据结构,希望我们能够更好地理解为什么使用它们。
那么,我们开始吧!
我首先想探讨的是一种名为B 树的数据结构,它是现代数据库设计的关键组成部分。
我们先来谈谈二叉搜索树。
传统上,排序地图一直是二叉搜索树(BST)的专属领域。关于二叉搜索树的文献、实现和在教育领域的推广可谓汗牛充栋。它们不仅引人深思,而且在理论和实践上都具有极高的应用价值,更拥有数以百万计的变体,足以满足各种需求。
二叉搜索树的基本思想是,树中的每个元素都对应一个单独的节点。每个节点都有两个指向子节点的指针,即左子节点和右子节点。左侧子树中的节点必须包含小于其父节点的元素,而右侧子树中的节点必须包含大于其父节点的元素。这使得搜索过程相当简单:从树的“根节点”开始,将该节点中的元素与搜索键进行比较。然后递归地搜索相应的左子树或右子树(如果找到完全匹配的元素则停止搜索)。
二叉搜索树有几种“类型”。例如,如果你使用红黑树,那么每个基本操作(搜索、插入、删除)的最坏情况时间复杂度都是对数级的,这非常棒!
但就计算机的实际运行方式而言,BST 存在一些严重的实际问题。许多应用程序,例如数据库和文件系统,其性能瓶颈并非在于 CPU 执行指令的速度,而是在于它访问磁盘数据的速度。归根结底,如今的 CPU 运行速度如此之快,以至于它们处理的数据必须速度极快且距离 CPU 非常近才能真正发挥作用。光速终究有限!此外,还需要考虑 CPU 可用的缓存,其缓存层级从“非常小但速度非常快”到“非常大但速度(相对而言)非常慢”不等。
缓存是如何工作的?简单来说……
缓存通常基于时空局部性假设工作。理想情况下,你需要的数据应该尽可能地彼此靠近。例如,如果你现在正在处理位于位置 A 的数据,理想情况下,你希望接下来的数据也位于位置 A 附近。一个很好的例子就是遍历数组:你想要的下一个数据实际上就在上一个数据旁边。由此可见,选择合适的数据结构至关重要。
这种假设通常大致是这样实现的:当请求内存中的 A 位置时,CPU 会检查它是否在最快的缓存中。如果在,那就太好了(缓存命中)!如果不在,那就糟了(缓存未命中),需要检查下一级(速度较慢、容量更大的)缓存。最坏的情况下,缓存会直接进入计算机的 RAM(或者更糟,直接进入磁盘!)。找到数据后,它会被添加到之前所有(容量较小、速度更快的)缓存级别,以及它周围的一些数据。然后,这个操作会驱逐一些被认为不太可能需要的数据。具体原理不在本文讨论范围内,但重点是:缓存命中速度很快,所以我们需要以时空局部的方式访问数据。为了更好地理解其规模,可以参考以下数据。
我们一开始聊的是二叉搜索树(BST),结果聊到了CPU和缓存命中/未命中。但是二叉搜索树是如何访问数据的呢?基本上是随机访问。树中的每个节点都与其他节点独立分配内存。因此,与数组不同,每个节点都位于内存中一个独立的区域,搜索操作实际上是一系列随机访问。粗略估计,每次从一个指针指向另一个指针时,都可能发生缓存未命中。真是糟糕!(就像荷兰人会说的那样!)
二叉搜索树实际上内存效率非常低。每个节点都有两个指针指向树中的每个元素。因此,在 64 位计算机上,这意味着每个元素都需要 16 字节的额外开销。更糟糕的是,其中一半的指针是空指针。而这还是在最佳情况下。如果考虑到填充以及节点需要存储的任何额外元数据(例如红黑树),二叉搜索树的内存效率就非常糟糕了。
更糟糕的是,对于二叉搜索树来说,每次插入都会触发内存分配。内存分配通常被认为是一种效率低下的操作,所以如果可以避免,我们当然会尽量避免!
B-Trees来帮忙啦!
什么是B树?以及为什么需要B树?
B树是一种自平衡树状数据结构,它能保持数据有序,并允许在对数时间内进行搜索、顺序访问、插入和删除操作。等等!这不就是二叉搜索树(BST)的功能吗?那我为什么还需要B树呢?
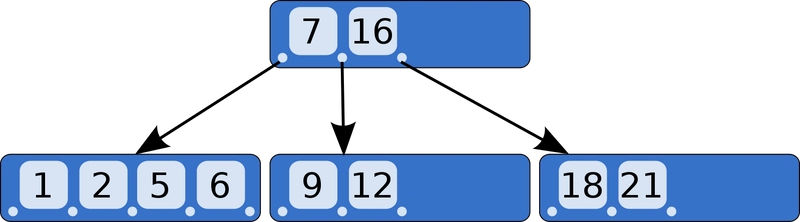
B 树借鉴了二叉搜索树 (BST) 的思想,简单来说,就是“我们不妨在里面加入一些数组,数组简单易用,计算机也喜欢数组,何乐而不为呢?”。因此,B 树的每个节点不再是包含一个元素和两个子节点,而是一个元素数组,每个元素又是一个子节点数组。所有元素都有序排列!
基本上,对于某个固定的常数B,每个节点包含B-1到2B-1 个元素,并按顺序排列(根节点可以只有一个元素)。一个包含k 个元素的内部节点(即有子节点的节点)有k+1个子节点。这样,每个元素仍然有一个“左”子节点和一个“右”子节点,但例如,第二个子节点包含的元素严格介于第一个元素和第二个元素之间。
根据Knuth 的定义,M 阶 B 树是满足以下性质的树:
- 每个节点最多有m个子节点。
- 除了根节点之外,每个非叶子节点至少有⌈M/2⌉个子节点。
- 如果根节点不是叶节点,则它至少有两个子节点。
- 具有k个子节点的非叶子节点包含k − 1 个键。
- 所有叶子都出现在同一层级,不携带任何信息。
每个内部节点的键值用作分隔值,用于划分其子树。例如,如果一个内部节点有 3 个子节点(或子树),则它必须有 2 个键值:_a1 和 _a2。最左侧子树中的所有值都小于 _a1,中间子树中的所有值都介于 _a1 和 _a2 之间,最右侧子树中的所有值都大于 _a2。
自1970 年发明以来,B 树作为一种存储在磁盘上的数据结构,历史上一直非常流行。这是因为访问磁盘可能非常缓慢,而 B 树可以一次性返回大量数据,这与二叉搜索树 (BST) 截然不同。搜索数据所需的 CPU 时间远少于从磁盘读取数据到内存所需的时间。例如,如果B = 1000,那么可以一次性在树中存储一千个条目,并在 RAM 中相对快速地处理它们。此外,与二叉搜索树相比,B 树的深度会非常浅,这意味着每次搜索可能只需要通过指针访问磁盘几次。听起来是不是很熟悉?这就是我们刚才讨论的缓存命中问题。
为了让您有个概念,以下是一些真实数据:
一个包含 10 万行数据的 SQLite 数据库使用深度为 3 的 B 树。因此,要获取一个节点,我们只需要读取 3 页或在节点之间跳转 3 次。如果使用二叉搜索树 (BST),则需要执行 log(100000) / log(2) = 16 次查找!这比 B 树的查找次数多了五倍多。我们当然不希望这样!
这些都很好,也很有趣,不过关于 B 树的理论就到此为止吧,让我们来看看 SQLite 是如何使用它的。如果您想更深入地了解 B 树及其在不同编程语言中的实现,我强烈推荐您阅读Open Data Structures。另一个提供大量 B 树背景知识的优秀资料来源是 Knuth 的《计算机程序设计艺术》第三卷“排序与搜索”,第 471-479 页。这是一本不错的轻松读物……
SQLite 使用 B 树来表示表和索引。但实际上,SQLite 使用了两种 B 树变体。传统的 B 树用于存储索引,称为“索引 B 树”。而 SQLite 则使用一种称为 B+ 树的变体来存储表,称为“表 B 树”。
主要区别在于,“表 B 树”或 B+ 树使用 64 位有符号整数键来引用内部节点中的数据,所有数据实际上都存储在叶子节点中。这个 64 位有符号整数被称为“行 ID (ROWID )”。此外,叶子节点可以包含指向下一个叶子节点的指针,以加快顺序访问速度。而“索引 B 树”或简称 B 树使用任意键,并且不存储任何数据。
以下是一些基本区别:
+-------------------------------+----------------+-----------------+
| # | B-tree | B+ tree |
+-------------------------------+----------------+-----------------+
| Pronounced | “Bee Tree” | “Bee Plus Tree” |
| Used to store | Indexes | Tables |
| Internal nodes store keys | Yes | Yes |
| Internal nodes store values | Yes | No |
| Number of children per node | Less | More |
| Internal nodes vs. leaf nodes | Same struct | Different struct|
+-------------------------------+----------------+-----------------+
另一个重要的信息是,SQLite 会在数据库中为数据库模式中的每个表(包括系统表,例如sqlite_schema )维护一个“表 B 树”。SQLite 还有一种名为WITHOUT_ROWID的表类型,但这里暂不赘述。此外,SQLite 还会为模式中的每个索引(包括由 UNIQUE 约束创建的隐式索引)维护一个“索引 B 树”。
让我们试着把它形象化!
假设数据库中存储了以下表格:
+-------+-------+-------+-----+
| ROWID | Name | Marks | Age |
+-------+-------+-------+-----+
| 6 | Jone | 5 | 28 |
| 15 | Alex | 32 | 45 |
| 12 | Tom | 37 | 23 |
| 53 | Ron | 87 | 13 |
| 24 | Mark | 20 | 48 |
| 25 | Bob | 89 | 32 |
+-------+-------+-------+-----+
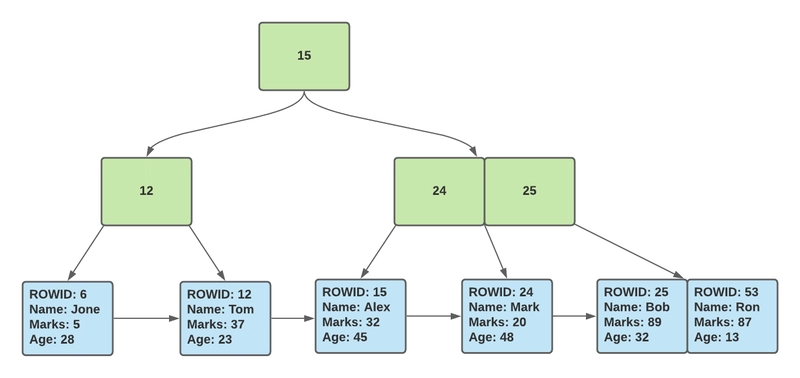
首先,数据库为每条记录创建一个唯一的自增索引(ROWID 或使用主键),并将相关行转换为字节流。然后,它将键和记录的字节流分别存储在 B+ 树中。这里,ROWID 用作索引键。键和记录的字节流统称为有效载荷。生成的 B+ 树可以表示如下。
如您所见,所有记录都存储在 B+ 树(或称“表 B 树”)的叶节点上,索引或 ROWID 用作创建 B+ 树的键。内部节点上不存储任何记录。每个叶节点都指向树中的下一条记录。这样,数据库既可以使用索引执行二分查找,也可以通过遍历每个元素进行顺序查找,而无需遍历叶节点。
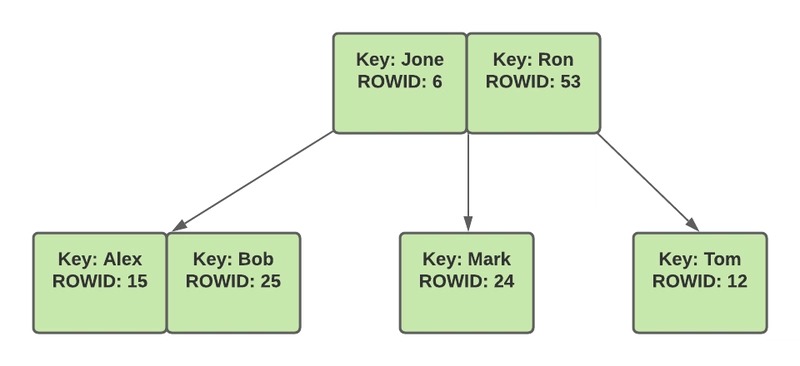
如果未使用索引,数据库将读取所有记录以查找指定记录。启用索引后,数据库会为表中的每个索引列创建一个 B 树或“索引 B 树”,如下所示。在本例中,我们对“名称”列创建了索引,并将该列值用作 B 树的键。索引是指向“表 B 树”中实际数据记录的引用。
当索引可用时,数据库引擎首先会在相应的索引 B 树中查找给定的键,并在对数时间内获取索引。然后,它会利用已找到的索引在表 B 树或 B+ 树中再次查找,同样在对数时间内完成,并返回记录。
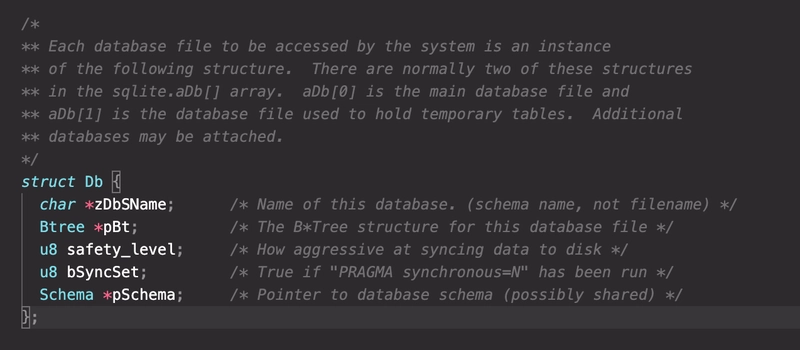
由于这次我们并没有真正进行任何编码,所以这里只是简单展示一下 SQLite 代码库中数据库的表示方式,顺便说一句,SQLite 代码库的注释和文档都非常完善。
这就是我们挚爱的 SQLite Btree,它代表着我们数据库的起点。如果我们深入研究这些属性,就会发现很多我们在文章中讨论过的内容。这里我就不赘述了,但如果你感兴趣,我强烈建议你去看看SQLite 的代码。
概括
我非常推崇第一性原理方法。运用第一性原理时,首先要确定要解决的问题,并定义一些约束条件和假设。一开始就定义约束条件的好处在于,它实际上定义了哪些事情不能做。而一旦明确了哪些事情不能做,哪些事情可以做就变得清晰明了。完成第一步后,将问题分解成更小的部分或其基本原理。最后,也是至关重要的一步,从零开始创建一个新的解决方案。
这一次,我们朝着理解问题迈出了非常重要的一步,通过定义一些数据结构的局限性来定义一些约束,甚至将问题分解成更小的部分,例如如何处理表和索引。
现在我们准备决定如何从头开始构建问题的解决方案,也就是说,我们究竟如何在 Rust 中构建数据结构。
← 第一部分 — 了解 SQLite 并设置 CLI 应用程序和 REPL
在 GitHub 上查看(非常欢迎提交 pull request)
如果你想关注我的动态,别忘了在Medium上关注我,也请给我点个赞!
其他来源:
- SQLite 的工作原理是什么?第二部分:B树!(或者说:磁盘寻道很慢,不要使用磁盘寻道!)
- Rust 集合案例研究:Alexis Beingessner 的 BTreeMap
- 让我们构建一个简单的数据库——第七部分——B树简介
- 开放数据结构——14.2 B树